Safe Haskell	None
Language	Haskell2010

Optics.AffineTraversal

Contents

Formation
Introduction
Elimination
Computation
Additional introduction forms
Additional elimination forms
Subtyping
van Laarhoven encoding

Description

An AffineTraversal is a Traversal that applies to at most one element.

These arise most frequently as the composition of a Lens with a Prism.

Synopsis

type AffineTraversal s t a b = Optic An_AffineTraversal NoIx s t a b
type AffineTraversal' s a = Optic' An_AffineTraversal NoIx s a
atraversal :: (s -> Either t a) -> (s -> b -> t) -> AffineTraversal s t a b
matching :: Is k An_AffineTraversal => Optic k is s t a b -> s -> Either t a
unsafeFiltered :: (a -> Bool) -> AffineTraversal' a a
withAffineTraversal :: Is k An_AffineTraversal => Optic k is s t a b -> ((s -> Either t a) -> (s -> b -> t) -> r) -> r
data An_AffineTraversal :: OpticKind
type AffineTraversalVL s t a b = forall f. Functor f => (forall r. r -> f r) -> (a -> f b) -> s -> f t
type AffineTraversalVL' s a = AffineTraversalVL s s a a
atraversalVL :: AffineTraversalVL s t a b -> AffineTraversal s t a b
toAtraversalVL :: Is k An_AffineTraversal => Optic k is s t a b -> AffineTraversalVL s t a b

Formation

type AffineTraversal s t a b = Optic An_AffineTraversal NoIx s t a b Source #

Type synonym for a type-modifying affine traversal.

type AffineTraversal' s a = Optic' An_AffineTraversal NoIx s a Source #

Type synonym for a type-preserving affine traversal.

Introduction

atraversal :: (s -> Either t a) -> (s -> b -> t) -> AffineTraversal s t a b Source #

Build an affine traversal from a matcher and an updater.

If you want to build an AffineTraversal from the van Laarhoven representation, use atraversalVL.

Elimination

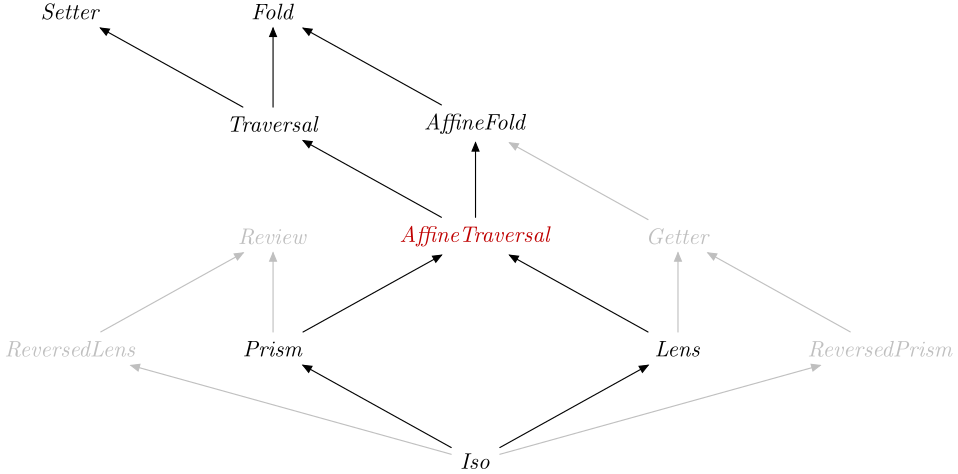
An AffineTraversal is in particular an AffineFold and a Setter, therefore you can specialise types to obtain:

preview :: AffineTraversal s t a b -> s -> Maybe a

over    :: AffineTraversal s t a b -> (a -> b) -> s -> t
set     :: AffineTraversal s t a b ->       b  -> s -> t

matching :: Is k An_AffineTraversal => Optic k is s t a b -> s -> Either t a Source #

Retrieve the value targeted by an AffineTraversal or return the original value while allowing the type to change if it does not match.

preview o ≡ either (const Nothing) id . matching o

Computation

matching (atraversal f g) ≡ f
isRight (f s)  =>  set (atraversal f g) b s ≡ g s b

Additional introduction forms

See _head, _tail, _init and _last for AffineTraversals for container types.

unsafeFiltered :: (a -> Bool) -> AffineTraversal' a a Source #

Filter result(s) of a traversal that don't satisfy a predicate.

Note: This is not a legal Traversal, unless you are very careful not to invalidate the predicate on the target.

As a counter example, consider that given evens = unsafeFiltered even the second Traversal law is violated:

over evens succ . over evens succ /= over evens (succ . succ)

So, in order for this to qualify as a legal Traversal you can only use it for actions that preserve the result of the predicate!

For a safe variant see indices (or filtered for read-only optics).

Additional elimination forms

withAffineTraversal :: Is k An_AffineTraversal => Optic k is s t a b -> ((s -> Either t a) -> (s -> b -> t) -> r) -> r Source #

Work with an affine traversal as a matcher and an updater.

Subtyping

data An_AffineTraversal :: OpticKind Source #

Tag for an affine traversal.

Instances

Is An_AffineTraversal A_Fold Source #
Instance details Defined in Optics.Internal.Optic.Subtyping Methods implies :: proxy An_AffineTraversal A_Fold p -> (Constraints An_AffineTraversal p -> r) -> Constraints A_Fold p -> r Source #
Is An_AffineTraversal An_AffineFold Source #
Instance details Defined in Optics.Internal.Optic.Subtyping Methods implies :: proxy An_AffineTraversal An_AffineFold p -> (Constraints An_AffineTraversal p -> r) -> Constraints An_AffineFold p -> r Source #
Is An_AffineTraversal A_Setter Source #
Instance details Defined in Optics.Internal.Optic.Subtyping Methods implies :: proxy An_AffineTraversal A_Setter p -> (Constraints An_AffineTraversal p -> r) -> Constraints A_Setter p -> r Source #
Is An_AffineTraversal A_Traversal Source #
Instance details Defined in Optics.Internal.Optic.Subtyping Methods implies :: proxy An_AffineTraversal A_Traversal p -> (Constraints An_AffineTraversal p -> r) -> Constraints A_Traversal p -> r Source #
Is A_Prism An_AffineTraversal Source #
Instance details Defined in Optics.Internal.Optic.Subtyping Methods implies :: proxy A_Prism An_AffineTraversal p -> (Constraints A_Prism p -> r) -> Constraints An_AffineTraversal p -> r Source #
Is A_Lens An_AffineTraversal Source #
Instance details Defined in Optics.Internal.Optic.Subtyping Methods implies :: proxy A_Lens An_AffineTraversal p -> (Constraints A_Lens p -> r) -> Constraints An_AffineTraversal p -> r Source #
Is An_Iso An_AffineTraversal Source #
Instance details Defined in Optics.Internal.Optic.Subtyping Methods implies :: proxy An_Iso An_AffineTraversal p -> (Constraints An_Iso p -> r) -> Constraints An_AffineTraversal p -> r Source #
ArrowChoice arr => ArrowOptic An_AffineTraversal arr Source #
Instance details Defined in Optics.Arrow Methods overA :: Optic An_AffineTraversal is s t a b -> arr a b -> arr s t Source #
ToReadOnly An_AffineTraversal s t a b Source #
Instance details Defined in Optics.ReadOnly Methods getting :: Optic An_AffineTraversal is s t a b -> Optic' (Join A_Getter An_AffineTraversal) is s a Source #
IxOptic An_AffineTraversal s t a b Source #
Instance details Defined in Optics.Indexed.Core Methods noIx :: NonEmptyIndices is => Optic An_AffineTraversal is s t a b -> Optic An_AffineTraversal NoIx s t a b Source #

AffineTraversal in the optics hierarchy

van Laarhoven encoding

type AffineTraversalVL s t a b = forall f. Functor f => (forall r. r -> f r) -> (a -> f b) -> s -> f t Source #

Type synonym for a type-modifying van Laarhoven affine traversal.

Note: this isn't exactly van Laarhoven representation as there is no Pointed class (which would be a superclass of Applicative that contains pure but not <*>). You can interpret the first argument as a dictionary of Pointed that supplies the point function (i.e. the implementation of pure).

A TraversalVL has Applicative available and hence can combine the effects arising from multiple elements using <*>. In contrast, an AffineTraversalVL has no way to combine effects from multiple elements, so it must act on at most one element. (It can act on none at all thanks to the availability of point.)

type AffineTraversalVL' s a = AffineTraversalVL s s a a Source #

Type synonym for a type-preserving van Laarhoven affine traversal.

atraversalVL :: AffineTraversalVL s t a b -> AffineTraversal s t a b Source #

Build an affine traversal from the van Laarhoven representation.

Example:

>>> :{
azSnd = atraversalVL $ \point f ab@(a, b) ->
  if a >= 'a' && a <= 'z'
  then (a, ) <$> f b
  else point ab
:}

>>> preview azSnd ('a', "Hi")
Just "Hi"

>>> preview azSnd ('@', "Hi")
Nothing

>>> over azSnd (++ "!!!") ('f', "Hi")
('f',"Hi!!!")

>>> set azSnd "Bye" ('Y', "Hi")
('Y',"Hi")

toAtraversalVL :: Is k An_AffineTraversal => Optic k is s t a b -> AffineTraversalVL s t a b Source #

Convert an affine traversal to its van Laarhoven representation.