Copyright	(C) 2019 Oleg Grenrus
License	BSD-3-Clause (see the file LICENSE)
Maintainer	Oleg Grenrus <oleg.grenrus@iki.fi>
Safe Haskell	Safe
Language	Haskell2010

Algebra.Lattice.M2

Description

Synopsis

data M2
- = M2o
- | M2a
- | M2b
- | M2i
toSetBool :: M2 -> Set Bool
fromSetBool :: Set Bool -> M2

Documentation

data M2 Source #

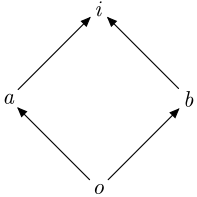
\(M_2\) is isomorphic to \(\mathcal{P}\{\mathbb{B}\}\), i.e. powerset of Bool.

Constructors

M2o
M2a
M2b
M2i

Instances

Bounded M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods minBound :: M2 # maxBound :: M2 #
Enum M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods succ :: M2 -> M2 # pred :: M2 -> M2 # toEnum :: Int -> M2 # fromEnum :: M2 -> Int # enumFrom :: M2 -> [M2] # enumFromThen :: M2 -> M2 -> [M2] # enumFromTo :: M2 -> M2 -> [M2] # enumFromThenTo :: M2 -> M2 -> M2 -> [M2] #
Eq M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods (==) :: M2 -> M2 -> Bool # (/=) :: M2 -> M2 -> Bool #
Data M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods gfoldl :: (forall d b. Data d => c (d -> b) -> d -> c b) -> (forall g. g -> c g) -> M2 -> c M2 # gunfold :: (forall b r. Data b => c (b -> r) -> c r) -> (forall r. r -> c r) -> Constr -> c M2 # toConstr :: M2 -> Constr # dataTypeOf :: M2 -> DataType # dataCast1 :: Typeable t => (forall d. Data d => c (t d)) -> Maybe (c M2) # dataCast2 :: Typeable t => (forall d e. (Data d, Data e) => c (t d e)) -> Maybe (c M2) # gmapT :: (forall b. Data b => b -> b) -> M2 -> M2 # gmapQl :: (r -> r' -> r) -> r -> (forall d. Data d => d -> r') -> M2 -> r # gmapQr :: (r' -> r -> r) -> r -> (forall d. Data d => d -> r') -> M2 -> r # gmapQ :: (forall d. Data d => d -> u) -> M2 -> [u] # gmapQi :: Int -> (forall d. Data d => d -> u) -> M2 -> u # gmapM :: Monad m => (forall d. Data d => d -> m d) -> M2 -> m M2 # gmapMp :: MonadPlus m => (forall d. Data d => d -> m d) -> M2 -> m M2 # gmapMo :: MonadPlus m => (forall d. Data d => d -> m d) -> M2 -> m M2 #
Ord M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods compare :: M2 -> M2 -> Ordering # (<) :: M2 -> M2 -> Bool # (<=) :: M2 -> M2 -> Bool # (>) :: M2 -> M2 -> Bool # (>=) :: M2 -> M2 -> Bool # max :: M2 -> M2 -> M2 # min :: M2 -> M2 -> M2 #
Read M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods readsPrec :: Int -> ReadS M2 # readList :: ReadS [M2] # readPrec :: ReadPrec M2 # readListPrec :: ReadPrec [M2] #
Show M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods showsPrec :: Int -> M2 -> ShowS # show :: M2 -> String # showList :: [M2] -> ShowS #
Generic M2 Source #
Instance details Defined in Algebra.Lattice.M2 Associated Types type Rep M2 :: Type -> Type # Methods from :: M2 -> Rep M2 x # to :: Rep M2 x -> M2 #
Function M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods function :: (M2 -> b) -> M2 :-> b #
Arbitrary M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods arbitrary :: Gen M2 # shrink :: M2 -> [M2] #
CoArbitrary M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods coarbitrary :: M2 -> Gen b -> Gen b #
NFData M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods rnf :: M2 -> () #
Hashable M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods hashWithSalt :: Int -> M2 -> Int # hash :: M2 -> Int #
Universe M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods universe :: [M2] #
Finite M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods universeF :: [M2] # cardinality :: Tagged M2 Natural #
PartialOrd M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods leq :: M2 -> M2 -> Bool Source # comparable :: M2 -> M2 -> Bool Source #
BoundedMeetSemiLattice M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods top :: M2 Source #
BoundedJoinSemiLattice M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods bottom :: M2 Source #
Lattice M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods (\/) :: M2 -> M2 -> M2 Source # (/\) :: M2 -> M2 -> M2 Source #
Heyting M2 Source #
Instance details Defined in Algebra.Lattice.M2 Methods (==>) :: M2 -> M2 -> M2 Source # neg :: M2 -> M2 Source # (<=>) :: M2 -> M2 -> M2 Source #
type Rep M2 Source #
Instance details Defined in Algebra.Lattice.M2 type Rep M2 = D1 (MetaData "M2" "Algebra.Lattice.M2" "lattices-2.0.2-HdMTcqWeXqlAAQvdNaFFrQ" False) ((C1 (MetaCons "M2o" PrefixI False) (U1 :: Type -> Type) :+: C1 (MetaCons "M2a" PrefixI False) (U1 :: Type -> Type)) :+: (C1 (MetaCons "M2b" PrefixI False) (U1 :: Type -> Type) :+: C1 (MetaCons "M2i" PrefixI False) (U1 :: Type -> Type)))

toSetBool :: M2 -> Set Bool Source #

fromSetBool :: Set Bool -> M2 Source #