| Safe Haskell | None |
|---|---|
| Language | Haskell2010 |
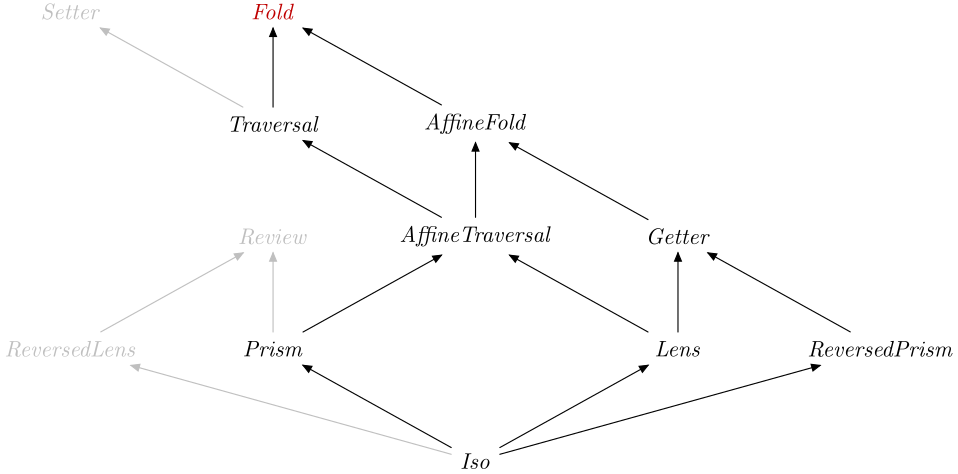
Optics.Fold
Contents
Description
A Fold S AA
from a container of type S. For example, toListOf can be used to obtain
the contained elements as a list. Unlike a Traversal,
there is no way to set or update elements.
This can be seen as a generalisation of traverse_, where the type S does
not need to be a type constructor with A as the last parameter.
A close relative is the AffineFold, which is a Fold
that contains at most one element.
Synopsis
- type Fold s a = Optic' A_Fold NoIx s a
- foldVL :: (forall f. Applicative f => (a -> f u) -> s -> f v) -> Fold s a
- foldOf :: (Is k A_Fold, Monoid a) => Optic' k is s a -> s -> a
- foldMapOf :: (Is k A_Fold, Monoid m) => Optic' k is s a -> (a -> m) -> s -> m
- foldrOf :: Is k A_Fold => Optic' k is s a -> (a -> r -> r) -> r -> s -> r
- foldlOf' :: Is k A_Fold => Optic' k is s a -> (r -> a -> r) -> r -> s -> r
- toListOf :: Is k A_Fold => Optic' k is s a -> s -> [a]
- sequenceOf_ :: (Is k A_Fold, Applicative f) => Optic' k is s (f a) -> s -> f ()
- traverseOf_ :: (Is k A_Fold, Applicative f) => Optic' k is s a -> (a -> f r) -> s -> f ()
- forOf_ :: (Is k A_Fold, Applicative f) => Optic' k is s a -> s -> (a -> f r) -> f ()
- folded :: Foldable f => Fold (f a) a
- folding :: Foldable f => (s -> f a) -> Fold s a
- foldring :: (forall f. Applicative f => (a -> f u -> f u) -> f v -> s -> f w) -> Fold s a
- unfolded :: (s -> Maybe (a, s)) -> Fold s a
- has :: Is k A_Fold => Optic' k is s a -> s -> Bool
- hasn't :: Is k A_Fold => Optic' k is s a -> s -> Bool
- headOf :: Is k A_Fold => Optic' k is s a -> s -> Maybe a
- lastOf :: Is k A_Fold => Optic' k is s a -> s -> Maybe a
- andOf :: Is k A_Fold => Optic' k is s Bool -> s -> Bool
- orOf :: Is k A_Fold => Optic' k is s Bool -> s -> Bool
- allOf :: Is k A_Fold => Optic' k is s a -> (a -> Bool) -> s -> Bool
- anyOf :: Is k A_Fold => Optic' k is s a -> (a -> Bool) -> s -> Bool
- noneOf :: Is k A_Fold => Optic' k is s a -> (a -> Bool) -> s -> Bool
- productOf :: (Is k A_Fold, Num a) => Optic' k is s a -> s -> a
- sumOf :: (Is k A_Fold, Num a) => Optic' k is s a -> s -> a
- asumOf :: (Is k A_Fold, Alternative f) => Optic' k is s (f a) -> s -> f a
- msumOf :: (Is k A_Fold, MonadPlus m) => Optic' k is s (m a) -> s -> m a
- elemOf :: (Is k A_Fold, Eq a) => Optic' k is s a -> a -> s -> Bool
- notElemOf :: (Is k A_Fold, Eq a) => Optic' k is s a -> a -> s -> Bool
- lengthOf :: Is k A_Fold => Optic' k is s a -> s -> Int
- maximumOf :: (Is k A_Fold, Ord a) => Optic' k is s a -> s -> Maybe a
- minimumOf :: (Is k A_Fold, Ord a) => Optic' k is s a -> s -> Maybe a
- maximumByOf :: Is k A_Fold => Optic' k is s a -> (a -> a -> Ordering) -> s -> Maybe a
- minimumByOf :: Is k A_Fold => Optic' k is s a -> (a -> a -> Ordering) -> s -> Maybe a
- findOf :: Is k A_Fold => Optic' k is s a -> (a -> Bool) -> s -> Maybe a
- findMOf :: (Is k A_Fold, Monad m) => Optic' k is s a -> (a -> m Bool) -> s -> m (Maybe a)
- lookupOf :: (Is k A_Fold, Eq a) => Optic' k is s (a, v) -> a -> s -> Maybe v
- pre :: Is k A_Fold => Optic' k is s a -> AffineFold s a
- backwards_ :: Is k A_Fold => Optic' k is s a -> Fold s a
- summing :: (Is k A_Fold, Is l A_Fold) => Optic' k is s a -> Optic' l js s a -> Fold s a
- failing :: (Is k A_Fold, Is l A_Fold) => Optic' k is s a -> Optic' l js s a -> Fold s a
- data A_Fold
Formation
Introduction
foldVL :: (forall f. Applicative f => (a -> f u) -> s -> f v) -> Fold s a Source #
Obtain a Fold by lifting traverse_ like function.
foldVL.traverseOf_≡idtraverseOf_.foldVL≡id
Elimination
foldOf :: (Is k A_Fold, Monoid a) => Optic' k is s a -> s -> a Source #
Combine the results of a fold using a monoid.
foldMapOf :: (Is k A_Fold, Monoid m) => Optic' k is s a -> (a -> m) -> s -> m Source #
Fold via embedding into a monoid.
foldrOf :: Is k A_Fold => Optic' k is s a -> (a -> r -> r) -> r -> s -> r Source #
Fold right-associatively.
foldlOf' :: Is k A_Fold => Optic' k is s a -> (r -> a -> r) -> r -> s -> r Source #
Fold left-associatively, and strictly.
sequenceOf_ :: (Is k A_Fold, Applicative f) => Optic' k is s (f a) -> s -> f () Source #
Evaluate each action in observed by a Fold on a structure from left to
right, ignoring the results.
sequenceA_≡sequenceOf_folded
>>>sequenceOf_ each (putStrLn "hello",putStrLn "world")hello world
traverseOf_ :: (Is k A_Fold, Applicative f) => Optic' k is s a -> (a -> f r) -> s -> f () Source #
Traverse over all of the targets of a Fold, computing an
Applicative-based answer, but unlike traverseOf do not
construct a new structure. traverseOf_ generalizes
traverse_ to work over any Fold.
>>>traverseOf_ each putStrLn ("hello","world")hello world
traverse_≡traverseOf_folded
forOf_ :: (Is k A_Fold, Applicative f) => Optic' k is s a -> s -> (a -> f r) -> f () Source #
A version of traverseOf_ with the arguments flipped.
Computation
traverseOf_(foldVLf) ≡ f
Additional introduction forms
foldring :: (forall f. Applicative f => (a -> f u -> f u) -> f v -> s -> f w) -> Fold s a Source #
Additional elimination forms
lengthOf :: Is k A_Fold => Optic' k is s a -> s -> Int Source #
Calculate the number of targets there are for a Fold in a given
container.
Note: This can be rather inefficient for large containers and just like
length, this will not terminate for infinite folds.
length≡lengthOffolded
>>>lengthOf _1 ("hello",())1
>>>lengthOf folded [1..10]10
>>>lengthOf (folded % folded) [[1,2],[3,4],[5,6]]6
maximumOf :: (Is k A_Fold, Ord a) => Optic' k is s a -> s -> Maybe a Source #
Obtain the maximum element (if any) targeted by a Fold safely.
Note: maximumOf on a valid Iso, Lens
or Getter will always return Just a value.
>>>maximumOf folded [1..10]Just 10
>>>maximumOf folded []Nothing
>>>maximumOf (folded % filtered even) [1,4,3,6,7,9,2]Just 6
maximum≡fromMaybe(error"empty").maximumOffolded
In the interest of efficiency, This operation has semantics more strict than
strictly necessary. \o -> has lazier
semantics but could leak memory.getMax . foldMapOf o Max
minimumOf :: (Is k A_Fold, Ord a) => Optic' k is s a -> s -> Maybe a Source #
Obtain the minimum element (if any) targeted by a Fold safely.
Note: minimumOf on a valid Iso, Lens
or Getter will always return Just a value.
>>>minimumOf folded [1..10]Just 1
>>>minimumOf folded []Nothing
>>>minimumOf (folded % filtered even) [1,4,3,6,7,9,2]Just 2
minimum≡fromMaybe(error"empty").minimumOffolded
In the interest of efficiency, This operation has semantics more strict than
strictly necessary. \o -> has lazier
semantics but could leak memory.getMin . foldMapOf o Min
maximumByOf :: Is k A_Fold => Optic' k is s a -> (a -> a -> Ordering) -> s -> Maybe a Source #
Obtain the maximum element (if any) targeted by a Fold according to a
user supplied Ordering.
>>>maximumByOf folded (compare `on` length) ["mustard","relish","ham"]Just "mustard"
In the interest of efficiency, This operation has semantics more strict than strictly necessary.
maximumBycmp ≡fromMaybe(error"empty").maximumByOffoldedcmp
minimumByOf :: Is k A_Fold => Optic' k is s a -> (a -> a -> Ordering) -> s -> Maybe a Source #
Obtain the minimum element (if any) targeted by a Fold according to a
user supplied Ordering.
In the interest of efficiency, This operation has semantics more strict than strictly necessary.
>>>minimumByOf folded (compare `on` length) ["mustard","relish","ham"]Just "ham"
minimumBycmp ≡fromMaybe(error"empty").minimumByOffoldedcmp
findMOf :: (Is k A_Fold, Monad m) => Optic' k is s a -> (a -> m Bool) -> s -> m (Maybe a) Source #
The findMOf function takes a Fold, a monadic predicate and a structure
and returns in the monad the leftmost element of the structure matching the
predicate, or Nothing if there is no such element.
>>>findMOf each (\x -> print ("Checking " ++ show x) >> return (even x)) (1,3,4,6)"Checking 1" "Checking 3" "Checking 4" Just 4
>>>findMOf each (\x -> print ("Checking " ++ show x) >> return (even x)) (1,3,5,7)"Checking 1" "Checking 3" "Checking 5" "Checking 7" Nothing
findMOffolded:: (Monad m, Foldable f) => (a -> m Bool) -> f a -> m (Maybe a)
lookupOf :: (Is k A_Fold, Eq a) => Optic' k is s (a, v) -> a -> s -> Maybe v Source #
The lookupOf function takes a Fold, a key, and a structure containing
key/value pairs. It returns the first value corresponding to the given
key. This function generalizes lookup to work on an arbitrary Fold
instead of lists.
>>>lookupOf folded 4 [(2, 'a'), (4, 'b'), (4, 'c')]Just 'b'
>>>lookupOf folded 2 [(2, 'a'), (4, 'b'), (4, 'c')]Just 'a'
Combinators
pre :: Is k A_Fold => Optic' k is s a -> AffineFold s a Source #
Convert a fold to an AffineFold that visits the first element of the
original fold.
backwards_ :: Is k A_Fold => Optic' k is s a -> Fold s a Source #
This allows you to traverse the elements of a Fold in the opposite order.
Semigroup structure
summing :: (Is k A_Fold, Is l A_Fold) => Optic' k is s a -> Optic' l js s a -> Fold s a infixr 6 Source #
Return entries of the first Fold, then the second one.
>>>toListOf (_1 % ix 0 `summing` _2 % ix 1) ([1,2], [4,7,1])[1,7]
failing :: (Is k A_Fold, Is l A_Fold) => Optic' k is s a -> Optic' l js s a -> Fold s a infixl 3 Source #
Try the first Fold. If it returns no entries, try the second one.
Subtyping
Tag for a fold.
Instances