| Copyright | (c) 2018 Oleg Grenrus |
|---|---|
| License | BSD-3-Clause |
| Safe Haskell | None |
| Language | Haskell2010 |
Topograph
Description
Tools to work with Directed Acyclic Graphs, by taking advantage of topological sorting.
Synopsis
- data G v i = G {
- gVertices :: [i]
- gFromVertex :: i -> v
- gToVertex :: v -> Maybe i
- gEdges :: i -> [i]
- gDiff :: i -> i -> Int
- gVerticeCount :: Int
- gVertexIndex :: i -> Int
- runG :: forall v r. Ord v => Map v (Set v) -> (forall i. Ord i => G v i -> r) -> Either [v] r
- runG' :: forall v r. Ord v => Map v (Set v) -> (forall i. Ord i => G v i -> r) -> Maybe r
- transpose :: forall v i. Ord i => G v i -> G v (Down i)
- reduction :: Ord i => G v i -> G v i
- closure :: Ord i => G v i -> G v i
- dfs :: forall v i. Ord i => G v i -> i -> [[i]]
- dfsTree :: forall v i. Ord i => G v i -> i -> Tree i
- allPaths :: forall v i. Ord i => G v i -> i -> i -> [[i]]
- allPaths' :: forall v i. Ord i => G v i -> i -> i -> [i] -> [[i]]
- allPathsTree :: forall v i. Ord i => G v i -> i -> i -> Maybe (Tree i)
- shortestPathLengths :: Ord i => G v i -> i -> [Int]
- longestPathLengths :: Ord i => G v i -> i -> [Int]
- edgesSet :: Ord i => G v i -> Set (i, i)
- adjacencyMap :: Ord v => G v i -> Map v (Set v)
- adjacencyList :: Ord v => G v i -> [(v, [v])]
- pairs :: [a] -> [(a, a)]
- treePairs :: Tree a -> [(a, a)]
Graph
Graph used in examples:
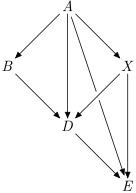
>>>let example :: Map Char (Set Char); example = Map.map Set.fromList $ Map.fromList [('a', "bxde"), ('b', "d"), ('x', "de"), ('d', "e"), ('e', "")]
>>>:set -XRecordWildCards>>>import Data.Monoid (All (..))>>>import Data.Foldable (traverse_)>>>import Data.List (elemIndex)>>>import Data.Tree (Tree (..))
Few functions to be used in examples
To make examples slightly shorter:
>>>let fmap2 = fmap . fmap>>>let fmap3 = fmap . fmap2>>>let traverse2_ = traverse_ . traverse_>>>let traverse3_ = traverse_ . traverse2_
To display trees:
>>>let dispTree :: Show a => Tree a -> IO (); dispTree = go 0 where go i (T.Node x xs) = putStrLn (replicate (i * 2) ' ' ++ show x) >> traverse_ (go (succ i)) xs
Graph representation.
The runG creates a G v ii is kept free,
so you cannot construct i which isn't in the gVertices.
Therefore operations, like gFromVertex are total (and fast).
Properties
gVerticeCountg =length(gVerticesg)
>>>runG example $ \G {..} -> (length gVertices, gVerticeCount)Right (5,5)
Just(gVertexIndexg x) =elemIndexx (gVerticesg)
>>>runG example $ \G {..} -> map (`elemIndex` gVertices) gVerticesRight [Just 0,Just 1,Just 2,Just 3,Just 4]
>>>runG example $ \G {..} -> map gVertexIndex gVerticesRight [0,1,2,3,4]
Constructors
| G | |
Fields
| |
Arguments
| :: Ord v | |
| => Map v (Set v) | Adjacency Map |
| -> (forall i. Ord i => G v i -> r) | function on linear indices |
| -> Either [v] r | Return the result or a cycle in the graph. |
Run action on topologically sorted representation of the graph.
Examples
Topological sorting
>>>runG example $ \G {..} -> map gFromVertex gVerticesRight "axbde"
Vertices are sorted
>>>runG example $ \G {..} -> map gFromVertex $ sort gVerticesRight "axbde"
Outgoing edges
>>>runG example $ \G {..} -> map (map gFromVertex . gEdges) gVerticesRight ["xbde","de","d","e",""]
Note: target indices are always larger than source vertex' index:
>>>runG example $ \G {..} -> getAll $ foldMap (\a -> foldMap (\b -> All (a < b)) (gEdges a)) gVerticesRight True
Not DAG
>>>let loop = Map.map Set.fromList $ Map.fromList [('a', "bx"), ('b', "cx"), ('c', "ax"), ('x', "")]>>>runG loop $ \G {..} -> map gFromVertex gVerticesLeft "abc"
>>>runG (Map.singleton 'a' (Set.singleton 'a')) $ \G {..} -> map gFromVertex gVerticesLeft "aa"
Transpose
transpose :: forall v i. Ord i => G v i -> G v (Down i) Source #
Graph with all edges reversed.
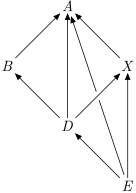
>>>runG example $ adjacencyList . transposeRight [('a',""),('b',"a"),('d',"abx"),('e',"adx"),('x',"a")]
Properties
Commutes with closure
>>>runG example $ adjacencyList . closure . transposeRight [('a',""),('b',"a"),('d',"abx"),('e',"abdx"),('x',"a")]
>>>runG example $ adjacencyList . transpose . closureRight [('a',""),('b',"a"),('d',"abx"),('e',"abdx"),('x',"a")]
Commutes with reduction
>>>runG example $ adjacencyList . reduction . transposeRight [('a',""),('b',"a"),('d',"bx"),('e',"d"),('x',"a")]
>>>runG example $ adjacencyList . transpose . reductionRight [('a',""),('b',"a"),('d',"bx"),('e',"d"),('x',"a")]
Transitive reduction
reduction :: Ord i => G v i -> G v i Source #
Transitive reduction.
Smallest graph, such that if there is a path from u to v in the original graph, then there is also such a path in the reduction.
The green edges are not in the transitive reduction:
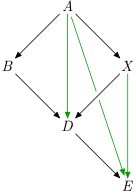
>>>runG example $ \g -> adjacencyList $ reduction gRight [('a',"bx"),('b',"d"),('d',"e"),('e',""),('x',"d")]
Taking closure first doesn't matter:
>>>runG example $ \g -> adjacencyList $ reduction $ closure gRight [('a',"bx"),('b',"d"),('d',"e"),('e',""),('x',"d")]
Transitive closure
closure :: Ord i => G v i -> G v i Source #
Transitive closure.
A graph, such that if there is a path from u to v in the original graph, then there is an edge from u to v in the closure.
The purple edge is added in a closure:
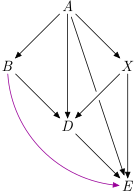
>>>runG example $ \g -> adjacencyList $ closure gRight [('a',"bdex"),('b',"de"),('d',"e"),('e',""),('x',"de")]
Taking reduction first, doesn't matter:
>>>runG example $ \g -> adjacencyList $ closure $ reduction gRight [('a',"bdex"),('b',"de"),('d',"e"),('e',""),('x',"de")]
DFS
dfs :: forall v i. Ord i => G v i -> i -> [[i]] Source #
Depth-first paths starting at a vertex.
>>>runG example $ \g@G{..} -> fmap3 gFromVertex $ dfs g <$> gToVertex 'x'Right (Just ["xde","xe"])
All paths
allPaths :: forall v i. Ord i => G v i -> i -> i -> [[i]] Source #
All paths from a to b. Note that every path has at least 2 elements, start and end.
Use allPaths' for the intermediate steps only.
See dfs, which returns all paths starting at some vertice.
This function returns paths with specified start and end vertices.
>>>runG example $ \g@G{..} -> fmap3 gFromVertex $ allPaths g <$> gToVertex 'a' <*> gToVertex 'e'Right (Just ["axde","axe","abde","ade","ae"])
There are no paths from element to itself:
>>>runG example $ \g@G{..} -> fmap3 gFromVertex $ allPaths g <$> gToVertex 'a' <*> gToVertex 'a'Right (Just [])
allPaths' :: forall v i. Ord i => G v i -> i -> i -> [i] -> [[i]] Source #
allPaths without begin and end elements.
>>>runG example $ \g@G{..} -> fmap3 gFromVertex $ allPaths' g <$> gToVertex 'a' <*> gToVertex 'e' <*> pure []Right (Just ["xd","x","bd","d",""])
allPathsTree :: forall v i. Ord i => G v i -> i -> i -> Maybe (Tree i) Source #
Like allPaths but return a Tree.
All paths from a to b. Note that every path has at least 2 elements, start and end,
Unfortunately, this is the same as dfs g <$> gToVertex 'a''a' end up in 'e'.
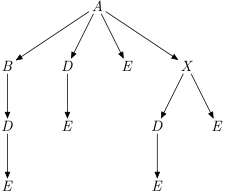
>>>let t = runG example $ \g@G{..} -> fmap3 gFromVertex $ allPathsTree g <$> gToVertex 'a' <*> gToVertex 'e'>>>fmap3 (T.foldTree $ \a bs -> if null bs then [[a]] else concatMap (map (a:)) bs) tRight (Just (Just ["axde","axe","abde","ade","ae"]))
>>>fmap3 (Set.fromList . treePairs) tRight (Just (Just (fromList [('a','b'),('a','d'),('a','e'),('a','x'),('b','d'),('d','e'),('x','d'),('x','e')])))
>>>let ls = runG example $ \g@G{..} -> fmap3 gFromVertex $ allPaths g <$> gToVertex 'a' <*> gToVertex 'e'>>>fmap2 (Set.fromList . concatMap pairs) lsRight (Just (fromList [('a','b'),('a','d'),('a','e'),('a','x'),('b','d'),('d','e'),('x','d'),('x','e')]))
Tree paths show how one can explore the paths.
>>>traverse3_ dispTree t'a' 'x' 'd' 'e' 'e' 'b' 'd' 'e' 'd' 'e' 'e'
>>>traverse3_ (putStrLn . T.drawTree . fmap show) t'a' | +- 'x' | | | +- 'd' | | | | | `- 'e' | | | `- 'e' ...
There are no paths from element to itself, but we'll return a
single root node, as Tree cannot be empty.
>>>runG example $ \g@G{..} -> fmap3 gFromVertex $ allPathsTree g <$> gToVertex 'a' <*> gToVertex 'a'Right (Just (Just (Node {rootLabel = 'a', subForest = []})))
Path lengths
shortestPathLengths :: Ord i => G v i -> i -> [Int] Source #
Shortest paths lengths starting from a vertex.
The resulting list is of the same length as gVertices.
It's quite efficient to compute all shortest (or longest) paths' lengths
at once. Zero means that there are no path.
>>>runG example $ \g@G{..} -> shortestPathLengths g <$> gToVertex 'a'Right (Just [0,1,1,1,1])
>>>runG example $ \g@G{..} -> shortestPathLengths g <$> gToVertex 'b'Right (Just [0,0,0,1,2])
longestPathLengths :: Ord i => G v i -> i -> [Int] Source #
Longest paths lengths starting from a vertex.
The resulting list is of the same length as gVertices.
>>>runG example $ \g@G{..} -> longestPathLengths g <$> gToVertex 'a'Right (Just [0,1,1,2,3])
>>>runG example $ \G {..} -> map gFromVertex gVerticesRight "axbde"
>>>runG example $ \g@G{..} -> longestPathLengths g <$> gToVertex 'b'Right (Just [0,0,0,1,2])
Query
edgesSet :: Ord i => G v i -> Set (i, i) Source #
Edges set.
>>>runG example $ \g@G{..} -> map (\(a,b) -> [gFromVertex a, gFromVertex b]) $ Set.toList $ edgesSet gRight ["ax","ab","ad","ae","xd","xe","bd","de"]
adjacencyMap :: Ord v => G v i -> Map v (Set v) Source #
Recover adjacency map representation from the G.
>>>runG example adjacencyMapRight (fromList [('a',fromList "bdex"),('b',fromList "d"),('d',fromList "e"),('e',fromList ""),('x',fromList "de")])
adjacencyList :: Ord v => G v i -> [(v, [v])] Source #
Adjacency list representation of G.
>>>runG example adjacencyListRight [('a',"bdex"),('b',"d"),('d',"e"),('e',""),('x',"de")]