Copyright	Written by David Himmelstrup
License	Unlicense
Maintainer	lemmih@gmail.com
Stability	experimental
Portability	POSIX
Safe Haskell	None
Language	Haskell2010

Reanimate.Morph.Linear

Description

Synopsis

linear :: Morph
rawLinear :: Morph
closestLinearCorrespondence :: PointCorrespondence
closestLinearCorrespondenceA :: (Real a, Fractional a, Epsilon a) => APolygon a -> APolygon a -> (APolygon a, APolygon a)
linearTrajectory :: Trajectory

Documentation

linear :: Morph Source #

Linear interpolation strategy.

Example:

playThenReverseA $ pauseAround 0.5 0.5 $ mkAnimation 3 $ \t ->
  withStrokeLineJoin JoinRound $
  let src = scale 8 $ center $ latex "X"
      dst = scale 8 $ center $ latex "H"
  in morph linear src dst t

rawLinear :: Morph Source #

Linear interpolation strategy without realigning corners. May give better results if the polygons are already aligned. Usually gives worse results.

Example:

playThenReverseA $ pauseAround 0.5 0.5 $ mkAnimation 3 $ \t ->
  withStrokeLineJoin JoinRound $
  let src = scale 8 $ center $ latex "X"
      dst = scale 8 $ center $ latex "H"
  in morph rawLinear src dst t

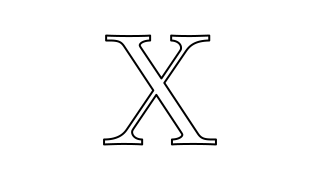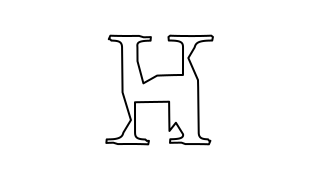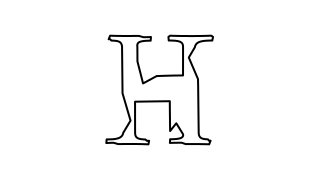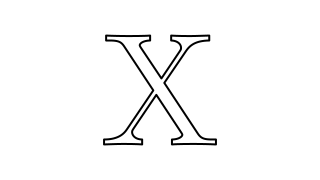
closestLinearCorrespondence :: PointCorrespondence Source #

Cycle polygons until the sum of the point trajectory path lengths is smallest.

closestLinearCorrespondenceA :: (Real a, Fractional a, Epsilon a) => APolygon a -> APolygon a -> (APolygon a, APolygon a) Source #

Cycle polygons until the sum of the point trajectory path lengths is smallest.

linearTrajectory :: Trajectory Source #

Strategy for moving points in a linear (straight-line) trajectory.