quipper-libraries-0.9.0.0: The standard libraries for Quipper.

Safe HaskellNone
LanguageHaskell98

Quipper.Libraries.Decompose.CliffordT

Contents

Description

This module provides transformers for decomposing circuits into the Clifford+T gate base.

  • Control trimming. This transformer uses doubly-controlled iX-gates to reduce the number of controls on gates. Specifically, it ensures that not-gates, Pauli X-, Y-, and Z-gates, and iX-gates have at most two controls; that phase gates of the form Diag(1, φ) have no controls; and that all other gates have at most one control.
  • Approximate Clifford+T decomposition. This decomposes all rotation and phase gates into Clifford+T up to a given precision ε, using an approximate synthesis algorithm. Other gates are unchanged.
  • Exact Clifford+T decomposition. This decomposes all gates that are exactly representable in the Clifford+T base into single-qubit Clifford gates, T, T†, and singly-controlled not-gates (with positive or negative control). Rotation and phase gates are left unchanged.
  • Standard gate set. We define the standard gate set to consist of the gates X, Y, Z, H, S, S†, T, T†, and CNOT. This transformer decomposes all gates that remain after applying both approximate and exact Clifford+T decomposition into the standard gate set. If the transformer encounters gates that are not single-qubit Clifford gates, T, T†, or singly-controlled not-gates (with positive or negative control), then the output is still semantically correct, but may not be in the standard gate set. This transformer suppresses global phases.
  • Strict gate set. We define the strict gate set to consist of the gates H, S, T, and CNOT. This transformer decomposes all gates that remain after applying both approximate and exact Clifford+T decomposition into the strict gate set. If the transformer encounters gates that are not single-qubit Clifford gates, T, T†, or singly-controlled not-gates (with positive or negative control), then the output is still semantically correct, but may not be in the strict gate set. This transformer suppresses global phases.

These above transformers may be applied in any order. Control trimming is primarily for demonstration purposes; it does not need to be combined with the other transformers as they do their own trimming. The exact and approximate Clifford+T decompositions can be applied in either order; since they each target a different set of gates, they must both be performed to obtain a complete decomposition into the Clifford+T gate set. The standard and strict transformers assume that their input has already been pre-processed by the exact and approximate transformers.

Synopsis

Auxiliary functions

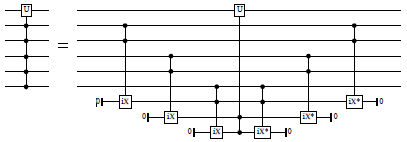
with_combined_controls_iX :: Int -> [Signed Endpoint] -> ([Signed Qubit] -> Circ a) -> Circ a Source #

A version of with_combined_controls that uses doubly-controlled iX-gates to do the decomposition. For example, when n=2, this yields circuits such as the following:

And for n=1:

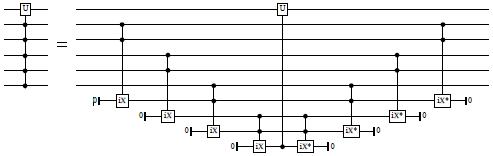
with_combined_controls_CT :: Int -> [Signed Endpoint] -> ([Signed Qubit] -> Circ a) -> Circ a Source #

A version of with_combined_controls_iX that further decomposes the doubly-controlled iX-gates into the Clifford+T gate base.

with_normalized_controls :: [Signed Endpoint] -> ([Qubit] -> Circ a) -> Circ a Source #

Turn a list of signed controls into a list of positive quantum controls, by applying all classical controls directly, and conjugating any negative quantum controls by X. Call the inner block with those quantum controls. Usage:

with_normalized_controls ctrls $ \qs -> do
  <<<code using qs>>>

with_normalized_controls_HS :: [Signed Endpoint] -> ([Qubit] -> Circ a) -> Circ a Source #

Like with_normalized_controls, but use HSSH instead of X, so as not to leave the H, S, T, CNot gate base.

negate_if :: Num r => Bool -> r -> r Source #

Negate the number if the boolean is true.

Transformers

Control trimming

trimcontrols_transformer :: Transformer Circ Qubit Bit Source #

This transformer makes sure that not-gates, Pauli X-, Y-, and Z-gates, and iX-gates have at most two controls; that phase gates of the form Diag(1, φ) have no controls; and that all other gates have at most one control.

Approximate Clifford+T decomposition

approx_ct_transformer :: RandomGen g => KeepPhase -> Precision -> g -> Transformer Circ Qubit Bit Source #

This transformer decomposes rotation and phase gates into the Clifford+T basis, using the approximate synthesis algorithm of http://arxiv.org/abs/1212.6253. Other gates are unchanged.

This transformer requires a precision parameter, as well as a source of randomness. The KeepPhase flag indicates whether to respect global phases.

Exact Clifford+T decomposition

exact_ct_transformer :: Transformer Circ Qubit Bit Source #

This transformer decomposes all gates that permit exact Clifford+T representations into the following concrete gate base for Clifford+T:

  • controlled-not (with one positive or negative control),
  • any single-qubit Clifford gates,
  • T and T†.

Classical controls and classical gates are not subject to the gate base, and are left untouched.

Rotations and phase gates are left unchanged by this transformer, but any controls on those gates will be decomposed.

Decomposition into standard gate set

standard_transformer :: Transformer Circ Qubit Bit Source #

This transformer decomposes a circuit into the standard gate set, which we define to be:

  • X, Y, Z, H, S, S†, T, T†, and CNOT.

As a precondition, the input circuit must only contain the following gates:

  • controlled-not (with one positive or negative control),
  • any single-qubit Clifford gates,
  • T and T†.

Global phases are suppressed. Classical controls and classical gates are not subject to the gate base, and are left untouched.

Any gates that are not among the input gates listed above will be transformed to a semantically correct circuit which may, however, contain gates that are not in the standard gate set. The best way to avoid this is to apply exact and approximate Clifford+T decomposition first.

Decomposition into strict gate set

strict_transformer :: Transformer Circ Qubit Bit Source #

This transformer decomposes a circuit into the strict gate set, which we define to be:

  • H, S, T, and CNOT.

As a precondition, the input circuit must only contain the following gates:

  • controlled-not (with one positive or negative control),
  • any single-qubit Clifford gates,
  • T and T†.

Global phases are suppressed. Classical controls and classical gates are not subject to the gate base, and are left untouched.

Any gates that are not among the input gates listed above will be transformed to a semantically correct circuit which may, however, contain gates that are not in the strict gate set. The best way to avoid this is to apply exact and approximate Clifford+T decomposition first.

Glue code for subroutines

The following is stuff we have to do because subroutines are not yet handled very abstractly. It is untested whether subroutines work at all.

trimcontrols_subroutine :: BoxId -> TypedSubroutine -> Circ () Source #

Handle subroutines for the trimcontrols_transformer.

trimcontrols_dtransformer :: DynamicTransformer Circ Qubit Bit Source #

Dynamic transformer for the trimcontrols_transformer.

trimcontrols_unary :: (QCData qa, QCData qb) => (qa -> Circ qb) -> qa -> Circ qb Source #

Unary transformer for the trimcontrols_transformer.

approx_ct_subroutine :: RandomGen g => KeepPhase -> Precision -> g -> BoxId -> TypedSubroutine -> Circ () Source #

Handle subroutines for the approx_ct_transformer.

approx_ct_dtransformer :: RandomGen g => KeepPhase -> Precision -> g -> DynamicTransformer Circ Qubit Bit Source #

Dynamic transformer for the approx_ct_transformer.

approx_ct_unary :: (RandomGen g, QCData qa, QCData qb) => KeepPhase -> Precision -> g -> (qa -> Circ qb) -> qa -> Circ qb Source #

Unary transformer for the approx_ct_transformer.

exact_ct_subroutine :: BoxId -> TypedSubroutine -> Circ () Source #

Handle subroutines for the exact_ct_transformer.

exact_ct_dtransformer :: DynamicTransformer Circ Qubit Bit Source #

Dynamic transformer for the exact_ct_transformer.

exact_ct_unary :: (QCData qa, QCData qb) => (qa -> Circ qb) -> qa -> Circ qb Source #

Unary transformer for the exact_ct_transformer.

standard_subroutine :: BoxId -> TypedSubroutine -> Circ () Source #

Handle subroutines for the standard_transformer.

standard_dtransformer :: DynamicTransformer Circ Qubit Bit Source #

Dynamic transformer for the standard_transformer.

standard_unary :: (QCData qa, QCData qb) => (qa -> Circ qb) -> qa -> Circ qb Source #

Unary transformer for the standard_transformer.

strict_subroutine :: BoxId -> TypedSubroutine -> Circ () Source #

Handle subroutines for the strict_transformer.

strict_dtransformer :: DynamicTransformer Circ Qubit Bit Source #

Dynamic transformer for the strict_transformer.

strict_unary :: (QCData qa, QCData qb) => (qa -> Circ qb) -> qa -> Circ qb Source #

Unary transformer for the strict_transformer.

Generic transformers

The following generic functions form the high-level interface to these decomposition transformers. This is how the transformers should be accessed by user code.

trimcontrols_generic :: (QCData qa, QCData qb, QCurry qfun qa qb) => qfun -> qfun Source #

This transformer makes sure that not-gates, Pauli X-, Y-, and Z-gates, and iX-gates have at most two controls; that phase gates of the form Diag(1, φ) have no controls; and that all other gates have at most one control.

approx_ct_generic :: (RandomGen g, QCData qa, QCData qb, QCurry qfun qa qb) => KeepPhase -> Precision -> g -> qfun -> qfun Source #

This transformer decomposes rotation and phase gates into the Clifford+T basis, using the approximate synthesis algorithm of http://arxiv.org/abs/1212.6253. It requires a precision parameter, as well as a source of randomness. Other gates are unchanged.

exact_ct_generic :: (QCData qa, QCData qb, QCurry qfun qa qb) => qfun -> qfun Source #

This transformer decomposes all gates that permit exact Clifford+T representations into the following concrete gate base for Clifford+T:

  • controlled-not (with one positive or negative control),
  • any single-qubit Clifford gates,
  • T and T†.

Classical controls and classical gates are not subject to the gate base, and are left untouched.

Rotations and phase gates are left unchanged by this transformer, but any controls on those gates will be decomposed.

standard_generic :: (QCData qa, QCData qb, QCurry qfun qa qb) => qfun -> qfun Source #

This transformer decomposes a circuit into the standard gate set, which we define to be:

  • X, Y, Z, H, S, S†, T, T†, and CNOT.

As a precondition, the input circuit must only contain the following gates:

  • controlled-not (with one positive or negative control),
  • any single-qubit Clifford gates,
  • T and T†.

Global phases are suppressed. Classical controls and classical gates are not subject to the gate base, and are left untouched.

Any gates that are not among the input gates listed above will be transformed to a semantically correct circuit which may, however, contain gates that are not in the standard gate set. The best way to avoid this is to apply exact and approximate Clifford+T decomposition first.

strict_generic :: (QCData qa, QCData qb, QCurry qfun qa qb) => qfun -> qfun Source #

This transformer decomposes a circuit into the strict gate set, which we define to be:

  • H, S, T, and CNOT.

As a precondition, the input circuit must only contain the following gates:

  • controlled-not (with one positive or negative control),
  • any single-qubit Clifford gates,
  • T and T†.

Global phases are suppressed. Classical controls and classical gates are not subject to the gate base, and are left untouched.

Any gates that are not among the input gates listed above will be transformed to a semantically correct circuit which may, however, contain gates that are not in the strict gate set. The best way to avoid this is to apply exact and approximate Clifford+T decomposition first.