| Safe Haskell | None |
|---|---|
| Language | Haskell2010 |
Data.Trie.Pattern
Contents
Description
A variant of a (radix) trie with the following characteristics:
- Keys are simple
Patterns composed ofMatchers and hence a single key can match multiple inputStrings. - Looking up a
matchfor aString canCaptureparts of the string. - Both patterns and input strings are understood as being composed of
(indivisible) chunks of strings of a generic type
s(typically instantiated to eitherTextorByteString). More precisely, every chunk of an inputString is tested against aMatcherof aPatternin sequence. As a result, pattern tries usually end up less compact than more general tries, since sharing of prefixes as well as all operations are limited to the granularity of these chunks.
These characteristics hint at the primary intended use-case, whereby keys have a "natural" decomposition into chunks and the same chunks are heavily shared by different keys, e.g. as in directory trees. A pattern trie allows to associate values with simple patterns, whereby a single value can essentially be looked up by all strings matching a pattern, thereby capturing parts of it.
Strictness:
A Trie is strict in the spine as well as the values (WHNF).
Ordering: The order of keys and thus elements is unspecified. No particular order may be assumed by folds and traversals, whose combining operations should hence be commutative.
Example:
>>>:set -XOverloadedStrings
>>>import Data.ByteString (ByteString)
>>>let p1 = mempty |> EqStr "home" |> EqStr "alice" |> EqStr "tmp">>>let p2 = mempty |> EqStr "home" |> AnyStr |> EqStr "music">>>let p3 = mempty |> EqStr "data" |> EqStr "bob" |> EqStr "books">>>let p4 = mempty |> EqStr "data" |> AnyStr |> EqStr "books">>>let p5 = mempty |> EqStr "data" |> AnyStr |> EqStr "books" |> EqStr "sicp"
>>>let trie = fromAssocList $ [p1,p2,p3,p4,p5] `zip` [1..] :: Trie ByteString Int
>>>match ["home","alice","tmp"] trieJust (1,fromList [])
>>>match ["home","bob","tmp"] trieNothing
>>>match ["home","alice","music"] trieJust (2,fromList [Capture {captured = "alice"}])
>>>match ["home","bob","music"] trieJust (2,fromList [Capture {captured = "bob"}])
>>>match ["data","bob","books"] trieJust (3,fromList [])
>>>match ["data","alice","books"] trieJust (4,fromList [Capture {captured = "alice"}])
>>>match ["data","alice","books","sicp"] trieJust (5,fromList [Capture {captured = "alice"}])
>>>match ["data","bob","books","sicp"] trieJust (5,fromList [Capture {captured = "bob"}])
>>>matchPrefix ["data","alice","books","wonderland"] trieJust (4,fromList [Capture {captured = "alice"}],["wonderland"])
>>>matchPrefix ["data","bob","books","wonderland"] trieJust (4,fromList [Capture {captured = "bob"}],["wonderland"])
>>>let (t,c,s) = matchPrefixTrie ["data","bob","books","wonderland"] trie>>>(value t, c, s)(Just 4,fromList [Capture {captured = "bob"}],["wonderland"])
Synopsis
- data Trie s a
- value :: Trie s a -> Maybe a
- type Pattern s = Seq (Matcher s)
- type Str s = [s]
- data Matcher s
- newtype Capture s = Capture {
- captured :: s
- overlapping :: Eq s => Pattern s -> Pattern s -> Bool
- newtype MatchOrd s = MatchOrd (Matcher s)
- newtype MatchPrefixOrd s = MatchPrefixOrd (Matcher s)
- matchOrd :: Pattern s -> Seq (MatchOrd s)
- matchPrefixOrd :: Pattern s -> Seq (MatchPrefixOrd s)
- apply :: Eq s => Str s -> Pattern s -> (Pattern s, Seq (Capture s), Str s)
- applyCapture :: Eq s => Str s -> Pattern s -> Seq (Capture s)
- unapplyCapture :: Pattern s -> Seq (Capture s) -> Str s
- applyMatch :: Eq s => Str s -> Pattern s -> Maybe (Seq (Capture s))
- applyMatches :: Eq s => Str s -> Pattern s -> Bool
- applyMatchPrefix :: Eq s => Str s -> Pattern s -> Maybe (Seq (Capture s))
- applyMatchesPrefix :: Eq s => Str s -> Pattern s -> Bool
- fromAssocList :: (Eq s, Hashable s) => [(Pattern s, a)] -> Trie s a
- toAssocList :: (Eq s, Hashable s) => Trie s a -> [(Pattern s, a)]
- insert :: (Eq s, Hashable s) => Pattern s -> a -> Trie s a -> Trie s a
- adjust :: (Eq s, Hashable s) => Pattern s -> (a -> a) -> Trie s a -> Trie s a
- delete :: (Eq s, Hashable s) => Pattern s -> Trie s a -> Trie s a
- lookup :: (Eq s, Hashable s) => Pattern s -> Trie s a -> Maybe a
- lookupPrefix :: (Eq s, Hashable s) => Pattern s -> Trie s a -> Maybe (a, Pattern s)
- lookupPrefixTrie :: (Eq s, Hashable s) => Pattern s -> Trie s a -> (Trie s a, Pattern s)
- match :: (Eq s, Hashable s) => Str s -> Trie s a -> Maybe (a, Seq (Capture s))
- matchPrefix :: (Eq s, Hashable s) => Str s -> Trie s a -> Maybe (a, Seq (Capture s), Str s)
- matchPrefixTrie :: (Eq s, Hashable s) => Str s -> Trie s a -> (Trie s a, Seq (Capture s), Str s)
- traverseWithKey :: Applicative f => (Pattern s -> a -> f b) -> Trie s a -> f (Trie s b)
- foldMapWithKey :: Monoid m => (Pattern s -> a -> m) -> Trie s a -> m
- foldrWithKey :: (Pattern s -> a -> b -> b) -> b -> Trie s a -> b
- (|>) :: Seq a -> a -> Seq a
Documentation
An unordered map from Patterns of strings of type s to values
of type a.
Instances
| Functor (Trie s) Source # | |
| Foldable (Trie s) Source # | |
Defined in Data.Trie.Pattern Methods fold :: Monoid m => Trie s m -> m # foldMap :: Monoid m => (a -> m) -> Trie s a -> m # foldr :: (a -> b -> b) -> b -> Trie s a -> b # foldr' :: (a -> b -> b) -> b -> Trie s a -> b # foldl :: (b -> a -> b) -> b -> Trie s a -> b # foldl' :: (b -> a -> b) -> b -> Trie s a -> b # foldr1 :: (a -> a -> a) -> Trie s a -> a # foldl1 :: (a -> a -> a) -> Trie s a -> a # elem :: Eq a => a -> Trie s a -> Bool # maximum :: Ord a => Trie s a -> a # minimum :: Ord a => Trie s a -> a # | |
| Traversable (Trie s) Source # | |
| (Eq s, Eq a) => Eq (Trie s a) Source # | |
| (Eq s, Hashable s, Read s, Read a) => Read (Trie s a) Source # | |
| (Show s, Show a) => Show (Trie s a) Source # | |
| Generic (Trie s a) Source # | |
| (Eq s, Hashable s) => Semigroup (Trie s a) Source # | Note (left preference): If two tries have a value attached to
the same |
| (Eq s, Hashable s) => Monoid (Trie s a) Source # | Note: |
| (NFData s, NFData a) => NFData (Trie s a) Source # | |
Defined in Data.Trie.Pattern | |
| type Rep (Trie s a) Source # | |
Defined in Data.Trie.Pattern type Rep (Trie s a) = D1 (MetaData "Trie" "Data.Trie.Pattern" "pattern-trie-0.1.0-D9GRwK2wxQCEPaAGzi8DAQ" False) (C1 (MetaCons "Trie" PrefixI True) (S1 (MetaSel (Just "strtries") NoSourceUnpackedness SourceStrict DecidedStrict) (Rec0 (HashMap s (Trie s a))) :*: (S1 (MetaSel (Just "vartrie") NoSourceUnpackedness SourceStrict DecidedStrict) (Rec0 (Maybe (Trie s a))) :*: S1 (MetaSel (Just "value") NoSourceUnpackedness SourceStrict DecidedStrict) (Rec0 (Maybe a))))) | |
value :: Trie s a -> Maybe a Source #
The value at the root of the trie, i.e.
value t == lookup mempty t
Patterns
Definition (Prefix Match): A String is a prefix match for a
Pattern, iff all Matchers in the pattern succeed when applied on
the chunks of the input string in sequence. A proper prefix match
is a prefix match that is not a (full) match.
A prefix match is witnessed by applyMatchesPrefix.
Definition ((Full) Match): A String is a (full) match for a
Pattern, iff it is a prefix match and there are no unmatched
remaining chunks of the input (i.e. the string and the pattern have
the same length).
A (full) match is witnessed by applyMatches.
Definition (Overlapping Patterns):
Two patterns are overlapping, iff they are not equal and
there exists an input String that is a (full) match for both patterns.
Overlapping patterns are witnessed by overlapping.
type Pattern s = Seq (Matcher s) Source #
A pattern is a sequence of Matchers and serves as a key in a pattern
trie.
If two patterns are overlapping for an input string, the preference for
a match is given by the partial order EqStr > AnyStr on the competing
matchers, i.e. towards the more specific pattern. This partial order is
witnessed and subsumed by the total order MatchOrd.
The preference for a prefix match is reversed, i.e. for an input string where
only a proper prefix is a match for overlapping patterns, the preference
is given by the partial order AnyStr > EqStr, i.e. towards the more general
pattern. This partial order is witnessed and subsumed by the total order
PrefixMatchOrd.
A Matcher is applied on a single chunk of an input String
while looking for a match and either succeeds or fails. If it succeeds,
it may Capture the chunk.
Constructors
| AnyStr | Match and capture an arbitrary chunk of an input string. |
| EqStr !s | Match a chunk of an input string exactly, capturing nothing. |
Instances
| Eq s => Eq (Matcher s) Source # | |
| Read s => Read (Matcher s) Source # | |
| Show s => Show (Matcher s) Source # | |
| Generic (Matcher s) Source # | |
| NFData s => NFData (Matcher s) Source # | |
Defined in Data.Trie.Pattern | |
| type Rep (Matcher s) Source # | |
Defined in Data.Trie.Pattern type Rep (Matcher s) = D1 (MetaData "Matcher" "Data.Trie.Pattern" "pattern-trie-0.1.0-D9GRwK2wxQCEPaAGzi8DAQ" False) (C1 (MetaCons "AnyStr" PrefixI False) (U1 :: * -> *) :+: C1 (MetaCons "EqStr" PrefixI False) (S1 (MetaSel (Nothing :: Maybe Symbol) NoSourceUnpackedness SourceStrict DecidedStrict) (Rec0 s))) | |
A captured chunk of an input String.
Instances
| Eq s => Eq (Capture s) Source # | |
| Ord s => Ord (Capture s) Source # | |
| Read s => Read (Capture s) Source # | |
| Show s => Show (Capture s) Source # | |
| Generic (Capture s) Source # | |
| NFData s => NFData (Capture s) Source # | |
Defined in Data.Trie.Pattern | |
| type Rep (Capture s) Source # | |
Defined in Data.Trie.Pattern | |
Testing Patterns
overlapping :: Eq s => Pattern s -> Pattern s -> Bool Source #
Check whether two patterns are overlapping, i.e. whether there
exists a String that is a (full) match for both patterns.
>>>let p1 = mempty |> EqStr "a" |> AnyStr>>>let p2 = mempty |> AnyStr |> EqStr "b">>>let p3 = mempty |> EqStr "a" |> EqStr "c">>>overlapping p1 p1False>>>overlapping p1 p2True>>>overlapping p1 p3True>>>overlapping p2 p3False
A total order for matchers that subsumes the partial order for
the preference between overlapping patterns on a match.
>>>MatchOrd AnyStr < MatchOrd (EqStr "a")True
>>>let p1 = mempty |> EqStr "a" |> EqStr "b">>>let p2 = mempty |> AnyStr |> EqStr "b">>>matchOrd p1 > matchOrd p2True
Instances
| Eq s => Eq (MatchOrd s) Source # | |
| Ord s => Ord (MatchOrd s) Source # | |
newtype MatchPrefixOrd s Source #
A total order for matchers that subsumes the partial order for
the preference between overlapping patterns on a matchPrefix.
>>>MatchPrefixOrd AnyStr > MatchPrefixOrd (EqStr "a")True
>>>let p1 = mempty |> EqStr "a" |> EqStr "b">>>let p2 = mempty |> AnyStr |> EqStr "b">>>matchPrefixOrd p1 < matchPrefixOrd p2True
Constructors
| MatchPrefixOrd (Matcher s) |
Instances
| Eq s => Eq (MatchPrefixOrd s) Source # | |
Defined in Data.Trie.Pattern Methods (==) :: MatchPrefixOrd s -> MatchPrefixOrd s -> Bool # (/=) :: MatchPrefixOrd s -> MatchPrefixOrd s -> Bool # | |
| Ord s => Ord (MatchPrefixOrd s) Source # | |
Defined in Data.Trie.Pattern Methods compare :: MatchPrefixOrd s -> MatchPrefixOrd s -> Ordering # (<) :: MatchPrefixOrd s -> MatchPrefixOrd s -> Bool # (<=) :: MatchPrefixOrd s -> MatchPrefixOrd s -> Bool # (>) :: MatchPrefixOrd s -> MatchPrefixOrd s -> Bool # (>=) :: MatchPrefixOrd s -> MatchPrefixOrd s -> Bool # max :: MatchPrefixOrd s -> MatchPrefixOrd s -> MatchPrefixOrd s # min :: MatchPrefixOrd s -> MatchPrefixOrd s -> MatchPrefixOrd s # | |
matchPrefixOrd :: Pattern s -> Seq (MatchPrefixOrd s) Source #
apply :: Eq s => Str s -> Pattern s -> (Pattern s, Seq (Capture s), Str s) Source #
Apply a string to a pattern, returning the unmatched suffix of the pattern together with the captured chunks and the remaining (unmatched) suffix of the input string.
>>>let p = mempty |> EqStr "a" |> AnyStr |> EqStr "c">>>let s = ["a", "b", "d"]>>>apply s p(fromList [EqStr "c"],fromList [Capture {captured = "b"}],["d"])
applyCapture :: Eq s => Str s -> Pattern s -> Seq (Capture s) Source #
Apply a string to a pattern, returning the captures.
>>>let p = mempty |> EqStr "a" |> AnyStr |> EqStr "c">>>let s = ["a", "b", "d"]>>>applyCapture s pfromList [Capture {captured = "b"}]
unapplyCapture :: Pattern s -> Seq (Capture s) -> Str s Source #
(Re)Construct the longest input String matching a prefix of a pattern,
using the given captures to satisfy matchers. As long as there are enough
captures to satisfy all matchers in the pattern, the resulting string will
always be a (full) match for the pattern.
Furthermore, if an input string s is a (full) match for a pattern p, then
unapplyCapture p (applyCapture s p) == s
>>>let p = mempty |> EqStr "a" |> AnyStr |> EqStr "c">>>let s = ["a", "b", "c"]>>>unapplyCapture p (applyCapture s p)["a","b","c"]
applyMatch :: Eq s => Str s -> Pattern s -> Maybe (Seq (Capture s)) Source #
Apply a string to a pattern, returning the captures iff the string is a (full) match for the pattern.
>>>let p = mempty |> EqStr "a" |> AnyStr |> EqStr "c">>>applyMatch ["a", "b", "c", "d"] pNothing>>>applyMatch ["a", "b", "c"] pJust (fromList [Capture {captured = "b"}])
applyMatches :: Eq s => Str s -> Pattern s -> Bool Source #
Apply a string to a pattern, returning True iff the string
is a (full) match for the pattern.
applyMatchPrefix :: Eq s => Str s -> Pattern s -> Maybe (Seq (Capture s)) Source #
Apply a string to a pattern, returning the captures iff the string is a prefix match for the pattern.
>>>let p = mempty |> EqStr "a" |> AnyStr |> EqStr "c">>>applyMatchPrefix ["a", "b", "c", "d"] pJust (fromList [Capture {captured = "b"}])
applyMatchesPrefix :: Eq s => Str s -> Pattern s -> Bool Source #
Apply a string to a pattern, returning True iff the string
is a prefix match for the pattern.
List conversion
fromAssocList :: (Eq s, Hashable s) => [(Pattern s, a)] -> Trie s a Source #
Create a pattern trie from a list of patterns and associated values.
\(\mathcal{O}(n \cdot k)\), where \(n\) is the length of the list and \(k\) is the length of the longest pattern in the list.
toAssocList :: (Eq s, Hashable s) => Trie s a -> [(Pattern s, a)] Source #
Create a list of patterns and associated values from a pattern trie.
\(\mathcal{O}(n \cdot k)\), where \(n\) is the number of values in the trie and \(k\) is the length of the longest pattern in the trie.
Modifications
insert :: (Eq s, Hashable s) => Pattern s -> a -> Trie s a -> Trie s a Source #
Insert the value for the given pattern into the trie.
\(\Theta(k)\), where \(k\) is the length of the pattern.
adjust :: (Eq s, Hashable s) => Pattern s -> (a -> a) -> Trie s a -> Trie s a Source #
Update the value of the given pattern in the trie, if it exists.
\(\mathcal{O}(k)\), where \(k\) is the length of the pattern.
delete :: (Eq s, Hashable s) => Pattern s -> Trie s a -> Trie s a Source #
Remove the value for the given pattern from the trie, if it exists.
\(\mathcal{O}(k)\), where \(k\) is the length of the pattern.
Pattern lookup
Time Complexity (successful lookups)
\(\Theta(k)\), where \(k\) is the length of the pattern.
lookup :: (Eq s, Hashable s) => Pattern s -> Trie s a -> Maybe a Source #
Lookup the value of a pattern.
If there is no value in the trie for the given pattern, the result is
Nothing.
lookupPrefix :: (Eq s, Hashable s) => Pattern s -> Trie s a -> Maybe (a, Pattern s) Source #
Lookup the value for the longest matching prefix of a pattern,
returning it together with the remaining suffix of the pattern.
If there is no value in the trie for any prefix of the given pattern,
the result is Nothing.
lookupPrefixTrie :: (Eq s, Hashable s) => Pattern s -> Trie s a -> (Trie s a, Pattern s) Source #
Lookup the trie rooted at the longest prefix of a pattern, returning it together with the remaining suffix of the pattern.
String matching
Time Complexity (successful matches)
In what follows \(k\) is always the length of the input string (i.e. the number of chunks).
Best case: \(\Theta(k)\), when the input string matches the most specific pattern in the trie (i.e. with the least captures) from all those that have a matching prefix for the string.
Worst case: \(\mathcal{O}(2^k)\), when there are \(2^{k-1}\) distinct
patterns of length at least \(k\) in the trie, all of which have a prefix of
length \(k-1\) that is a prefix match for the input string, but none except
for the most general of them are an actual (full) match. This is a
pathological case that comes about from backtracking to more general patterns
and is illustrated in an example with \(k=3\) for the input string
["a","a","b"] below.
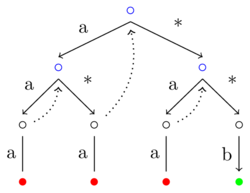
Nodes with values are filled, choice points are blue, dead ends are red and dashed lines indicate backtracking. The above trie contains the keys (patterns)
mempty |> EqStr "a" |> EqStr "a" |> EqStr "a"
mempty |> EqStr "a" |> AnyStr |> EqStr "a"
mempty |> AnyStr |> EqStr "a" |> EqStr "a"
mempty |> AnyStr |> AnyStr |> EqStr "b"
with some arbitrary values. The paths are explored left-to-right in a depth-first search. The number of steps for a match in the worst case is more accurately approximated by \[ \underbrace{2^k - 1}_{\text{downwards searching}} + \underbrace{2^{k-1} - 1}_{\text{upwards backtracking}} \] Dropping the asymptotically insignificant constants and lower terms yields the bound. For realistic values of \(k\), however, the difference matters.
match :: (Eq s, Hashable s) => Str s -> Trie s a -> Maybe (a, Seq (Capture s)) Source #
Lookup the value for an input string by matching it against the patterns of
a trie. The value of the matching pattern, if any, is returned together with
any captured parts of the input string. If the input string does not match
any pattern in the trie, the result is Nothing.
matchPrefix :: (Eq s, Hashable s) => Str s -> Trie s a -> Maybe (a, Seq (Capture s), Str s) Source #
Lookup the value for the longest matching prefix of the input string,
returning it together with any captured parts and the remaining
(unmatched) suffix of the input string. If no prefix of the input
string matches any pattern in the trie, the result is Nothing.
matchPrefixTrie :: (Eq s, Hashable s) => Str s -> Trie s a -> (Trie s a, Seq (Capture s), Str s) Source #
Lookup the trie rooted at the longest matching prefix of the input string, returning it together with any captured parts and the remaining (unmatched) suffix of the input string.
In particular, if the input string is a (full) match for a pattern, the
returned trie is the subtrie that is rooted at the associated value.
Special folds and traversals
traverseWithKey :: Applicative f => (Pattern s -> a -> f b) -> Trie s a -> f (Trie s b) Source #
foldrWithKey :: (Pattern s -> a -> b -> b) -> b -> Trie s a -> b Source #