| Safe Haskell | None |
|---|---|
| Language | Haskell2010 |
Optics.Traversal
Contents
Description
A Traversal lifts an effectful operation on elements to act on structures
containing those elements.
That is, given a function op :: A -> F B where F is Applicative, a
Traversal S T A BS -> F T that applies op to
all the As contained in the S.
This can be seen as a generalisation of traverse, where the type S does
not need to be a type constructor with A as the last parameter.
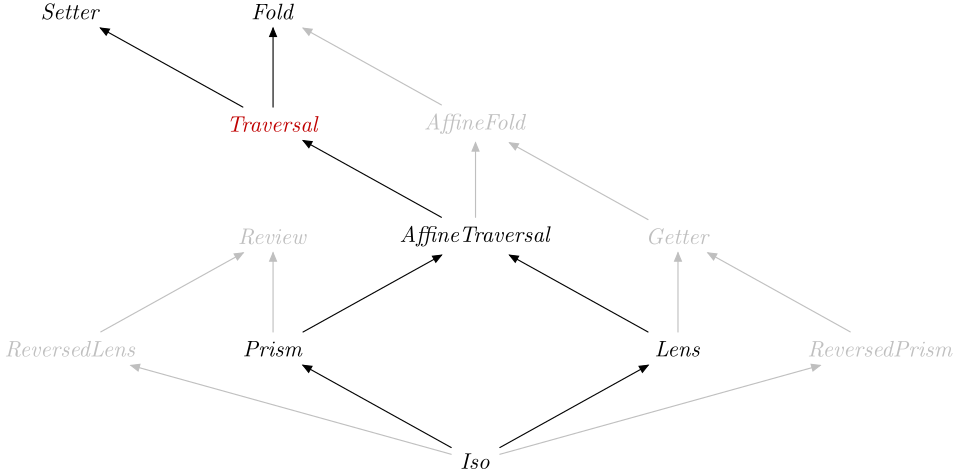
A Lens is a Traversal that acts on a single value.
A close relative is the AffineTraversal, which is a
Traversal that acts on at most one value.
Synopsis
- type Traversal s t a b = Optic A_Traversal NoIx s t a b
- type Traversal' s a = Optic' A_Traversal NoIx s a
- traversalVL :: TraversalVL s t a b -> Traversal s t a b
- traverseOf :: (Is k A_Traversal, Applicative f) => Optic k is s t a b -> (a -> f b) -> s -> f t
- traversed :: Traversable t => Traversal (t a) (t b) a b
- forOf :: (Is k A_Traversal, Applicative f) => Optic k is s t a b -> s -> (a -> f b) -> f t
- sequenceOf :: (Is k A_Traversal, Applicative f) => Optic k is s t (f b) b -> s -> f t
- transposeOf :: Is k A_Traversal => Optic k is s t [a] a -> s -> [t]
- mapAccumROf :: Is k A_Traversal => Optic k is s t a b -> (acc -> a -> (b, acc)) -> acc -> s -> (t, acc)
- mapAccumLOf :: Is k A_Traversal => Optic k is s t a b -> (acc -> a -> (b, acc)) -> acc -> s -> (t, acc)
- scanr1Of :: Is k A_Traversal => Optic k is s t a a -> (a -> a -> a) -> s -> t
- scanl1Of :: Is k A_Traversal => Optic k is s t a a -> (a -> a -> a) -> s -> t
- failover :: Is k A_Traversal => Optic k is s t a b -> (a -> b) -> s -> Maybe t
- failover' :: Is k A_Traversal => Optic k is s t a b -> (a -> b) -> s -> Maybe t
- backwards :: Is k A_Traversal => Optic k is s t a b -> Traversal s t a b
- partsOf :: forall k is s t a. Is k A_Traversal => Optic k is s t a a -> Lens s t [a] [a]
- data A_Traversal
- type TraversalVL s t a b = forall f. Applicative f => (a -> f b) -> s -> f t
- type TraversalVL' s a = TraversalVL s s a a
Formation
type Traversal s t a b = Optic A_Traversal NoIx s t a b Source #
Type synonym for a type-modifying traversal.
type Traversal' s a = Optic' A_Traversal NoIx s a Source #
Type synonym for a type-preserving traversal.
Introduction
traversalVL :: TraversalVL s t a b -> Traversal s t a b Source #
Build a traversal from the van Laarhoven representation.
traversalVL.traverseOf≡idtraverseOf.traversalVL≡id
Elimination
traverseOf :: (Is k A_Traversal, Applicative f) => Optic k is s t a b -> (a -> f b) -> s -> f t Source #
Map each element of a structure targeted by a Traversal, evaluate these
actions from left to right, and collect the results.
Computation
traverseOf(traversalVLf) ≡ f
Well-formedness
traverseOfopure≡purefmap(traverseOfo f) .traverseOfo g ≡getCompose.traverseOfo (Compose.fmapf . g)
Additional introduction forms
traversed :: Traversable t => Traversal (t a) (t b) a b Source #
Construct a Traversal via the Traversable class.
traverseOftraversed=traverse
Additional elimination forms
forOf :: (Is k A_Traversal, Applicative f) => Optic k is s t a b -> s -> (a -> f b) -> f t Source #
A version of traverseOf with the arguments flipped.
sequenceOf :: (Is k A_Traversal, Applicative f) => Optic k is s t (f b) b -> s -> f t Source #
Evaluate each action in the structure from left to right, and collect the results.
>>>sequenceOf each ([1,2],[3,4])[(1,3),(1,4),(2,3),(2,4)]
sequence≡sequenceOftraversed≡traverseidsequenceOfo ≡traverseOfoid
transposeOf :: Is k A_Traversal => Optic k is s t [a] a -> s -> [t] Source #
mapAccumROf :: Is k A_Traversal => Optic k is s t a b -> (acc -> a -> (b, acc)) -> acc -> s -> (t, acc) Source #
This generalizes mapAccumR to an arbitrary Traversal.
mapAccumR≡mapAccumROftraversed
mapAccumROf accumulates State from right to left.
mapAccumLOf :: Is k A_Traversal => Optic k is s t a b -> (acc -> a -> (b, acc)) -> acc -> s -> (t, acc) Source #
This generalizes mapAccumL to an arbitrary Traversal.
mapAccumL≡mapAccumLOftraverse
mapAccumLOf accumulates State from left to right.
failover :: Is k A_Traversal => Optic k is s t a b -> (a -> b) -> s -> Maybe t Source #
Try to map a function over this Traversal, returning Nothing if the
traversal has no targets.
>>>failover (element 3) (*2) [1,2]Nothing
>>>failover _Left (*2) (Right 4)Nothing
>>>failover _Right (*2) (Right 4)Just (Right 8)
failover' :: Is k A_Traversal => Optic k is s t a b -> (a -> b) -> s -> Maybe t Source #
Version of failover strict in the application of f.
Combinators
backwards :: Is k A_Traversal => Optic k is s t a b -> Traversal s t a b Source #
This allows you to traverse the elements of a traversal in the opposite
order.
partsOf :: forall k is s t a. Is k A_Traversal => Optic k is s t a a -> Lens s t [a] [a] Source #
partsOf turns a Traversal into a Lens.
Note: You should really try to maintain the invariant of the number of children in the list.
>>>('a','b','c') & partsOf each .~ ['x','y','z']('x','y','z')
Any extras will be lost. If you do not supply enough, then the remainder will come from the original structure.
>>>('a','b','c') & partsOf each .~ ['w','x','y','z']('w','x','y')
>>>('a','b','c') & partsOf each .~ ['x','y']('x','y','c')
>>>('b', 'a', 'd', 'c') & partsOf each %~ sort('a','b','c','d')
So technically, this is only a Lens if you do not change the number of
results it returns.
Subtyping
data A_Traversal Source #
Tag for a traversal.
Instances
van Laarhoven encoding
The van Laarhoven representation of a Traversal directly expresses how
it lifts an effectful operation A -> F B on elements to act on structures
S -> F T. Thus traverseOf converts a Traversal to a TraversalVL.
type TraversalVL s t a b = forall f. Applicative f => (a -> f b) -> s -> f t Source #
Type synonym for a type-modifying van Laarhoven traversal.
type TraversalVL' s a = TraversalVL s s a a Source #
Type synonym for a type-preserving van Laarhoven traversal.