| Copyright | (C) Frank Staals |
|---|---|
| License | see the LICENSE file |
| Maintainer | Frank Staals |
| Safe Haskell | None |
| Language | Haskell2010 |
Data.PlaneGraph.Core
Description
Data type for planar graphs embedded in \(\mathbb{R}^2\). For functions that export faces and edges etc, we assume the graph has a (planar) straight line embedding.
Synopsis
- newtype PlaneGraph s v e f r = PlaneGraph (PlanarGraph s Primal (VertexData r v) e f)
- graph :: forall k (s :: k) v e f r k (s :: k) v e f r. Iso (PlaneGraph (s :: k) v e f r) (PlaneGraph (s :: k) v e f r) (PlanarGraph s 'Primal (VertexData r v) e f) (PlanarGraph s 'Primal (VertexData r v) e f)
- data PlanarGraph (s :: k) (w :: World) v e f
- data VertexData r v = VertexData !(Point 2 r) !v
- vData :: forall r v v. Lens (VertexData r v) (VertexData r v) v v
- location :: forall r v r. Lens (VertexData r v) (VertexData r v) (Point 2 r) (Point 2 r)
- vtxDataToExt :: VertexData r v -> Point 2 r :+ v
- fromSimplePolygon :: proxy s -> SimplePolygon p r -> f -> f -> PlaneGraph s p () f r
- fromConnectedSegments :: (Foldable f, Ord r, Num r) => proxy s -> f (LineSegment 2 p r :+ e) -> PlaneGraph s (NonEmpty p) e () r
- fromAdjacencyLists :: forall k (s :: k) (w :: World) h. (Foldable h, Functor h) => [(VertexId s w, h (VertexId s w))] -> PlanarGraph s w () () ()
- numVertices :: PlaneGraph s v e f r -> Int
- numEdges :: PlaneGraph s v e f r -> Int
- numFaces :: PlaneGraph s v e f r -> Int
- numDarts :: PlaneGraph s v e f r -> Int
- dual :: forall k (s :: k) (w :: World) v e f. Getter (PlanarGraph s w v e f) (PlanarGraph s (DualOf w) f e v)
- vertices' :: PlaneGraph s v e f r -> Vector (VertexId' s)
- vertices :: PlaneGraph s v e f r -> Vector (VertexId' s, VertexData r v)
- edges' :: PlaneGraph s v e f r -> Vector (Dart s)
- edges :: PlaneGraph s v e f r -> Vector (Dart s, e)
- faces' :: PlaneGraph s v e f r -> Vector (FaceId' s)
- faces :: PlaneGraph s v e f r -> Vector (FaceId' s, f)
- internalFaces :: (Ord r, Fractional r) => PlaneGraph s v e f r -> Vector (FaceId' s, f)
- faces'' :: (Ord r, Fractional r) => PlaneGraph s v e f r -> ((FaceId' s, f), Vector (FaceId' s, f))
- darts' :: PlaneGraph s v e f r -> Vector (Dart s)
- darts :: PlaneGraph s v e f r -> Vector (Dart s, e)
- traverseVertices :: Applicative m => (VertexId' s -> v -> m v') -> PlaneGraph s v e f r -> m (PlaneGraph s v' e f r)
- traverseDarts :: Applicative m => (Dart s -> e -> m e') -> PlaneGraph s v e f r -> m (PlaneGraph s v e' f r)
- traverseFaces :: Applicative m => (FaceId' s -> f -> m f') -> PlaneGraph s v e f r -> m (PlaneGraph s v e f' r)
- headOf :: Dart s -> PlaneGraph s v e f r -> VertexId' s
- tailOf :: Dart s -> PlaneGraph s v e f r -> VertexId' s
- twin :: forall k (s :: k). Dart s -> Dart s
- endPoints :: Dart s -> PlaneGraph s v e f r -> (VertexId' s, VertexId' s)
- incidentEdges :: VertexId' s -> PlaneGraph s v e f r -> Vector (Dart s)
- incomingEdges :: VertexId' s -> PlaneGraph s v e f r -> Vector (Dart s)
- outgoingEdges :: VertexId' s -> PlaneGraph s v e f r -> Vector (Dart s)
- neighboursOf :: VertexId' s -> PlaneGraph s v e f r -> Vector (VertexId' s)
- nextIncidentEdge :: Dart s -> PlaneGraph s v e f r -> Dart s
- prevIncidentEdge :: Dart s -> PlaneGraph s v e f r -> Dart s
- leftFace :: Dart s -> PlaneGraph s v e f r -> FaceId' s
- rightFace :: Dart s -> PlaneGraph s v e f r -> FaceId' s
- nextEdge :: Dart s -> PlaneGraph s v e f r -> Dart s
- prevEdge :: Dart s -> PlaneGraph s v e f r -> Dart s
- boundary :: FaceId' s -> PlaneGraph s v e f r -> Vector (Dart s)
- boundary' :: Dart s -> PlaneGraph s v e f r -> Vector (Dart s)
- boundaryDart :: FaceId' s -> PlaneGraph s v e f r -> Dart s
- boundaryVertices :: FaceId' s -> PlaneGraph s v e f r -> Vector (VertexId' s)
- outerFaceId :: (Ord r, Fractional r) => PlaneGraph s v e f r -> FaceId' s
- outerFaceDart :: (Ord r, Fractional r) => PlaneGraph s v e f r -> Dart s
- vertexDataOf :: VertexId' s -> Lens' (PlaneGraph s v e f r) (VertexData r v)
- locationOf :: VertexId' s -> Lens' (PlaneGraph s v e f r) (Point 2 r)
- class HasDataOf g i where
- endPointsOf :: Dart s -> Getter (PlaneGraph s v e f r) (VertexData r v, VertexData r v)
- endPointData :: Dart s -> PlaneGraph s v e f r -> (VertexData r v, VertexData r v)
- vertexData :: Lens (PlaneGraph s v e f r) (PlaneGraph s v' e f r) (Vector v) (Vector v')
- faceData :: Lens (PlaneGraph s v e f r) (PlaneGraph s v e f' r) (Vector f) (Vector f')
- dartData :: Lens (PlaneGraph s v e f r) (PlaneGraph s v e' f r) (Vector (Dart s, e)) (Vector (Dart s, e'))
- rawDartData :: Lens (PlaneGraph s v e f r) (PlaneGraph s v e' f r) (Vector e) (Vector e')
- edgeSegment :: Dart s -> PlaneGraph s v e f r -> LineSegment 2 v r :+ e
- edgeSegments :: PlaneGraph s v e f r -> Vector (Dart s, LineSegment 2 v r :+ e)
- rawFacePolygon :: FaceId' s -> PlaneGraph s v e f r -> SimplePolygon v r :+ f
- rawFaceBoundary :: FaceId' s -> PlaneGraph s v e f r -> SimplePolygon v r :+ f
- rawFacePolygons :: PlaneGraph s v e f r -> Vector (FaceId' s, SimplePolygon v r :+ f)
- newtype VertexId (s :: k) (w :: World) = VertexId {
- _unVertexId :: Int
- newtype FaceId (s :: k) (w :: World) = FaceId {}
- data Dart (s :: k)
- data World
- type VertexId' (s :: k) = VertexId s 'Primal
- type FaceId' (s :: k) = FaceId s 'Primal
- withEdgeDistances :: (Point 2 r -> Point 2 r -> a) -> PlaneGraph s p e f r -> PlaneGraph s p (a :+ e) f r
Documentation
>>>import Data.Proxy>>>import Data.PlaneGraph.AdjRep(Gr(Gr),Face(Face),Vtx(Vtx))>>>import Data.PlaneGraph.IO(fromAdjRep)>>>import Data.PlanarGraph.Dart(Dart(..),Arc(..))>>>:{let dart i s = Dart (Arc i) (read s) small :: Gr (Vtx Int String Int) (Face String) small = Gr [ Vtx 0 (Point2 0 0) [ (2,"0->2") , (1,"0->1") , (3,"0->3") ] 0 , Vtx 1 (Point2 2 2) [ (0,"1->0") , (2,"1->2") , (3,"1->3") ] 1 , Vtx 2 (Point2 2 0) [ (0,"2->0") , (1,"2->1") ] 2 , Vtx 3 (Point2 (-1) 4) [ (0,"3->0") , (1,"3->1") ] 3 ] [ Face (2,1) "OuterFace" , Face (0,1) "A" , Face (1,0) "B" ] smallG = fromAdjRep (Proxy :: Proxy ()) small :}
This represents the following graph. Note that the graph is undirected, the arrows are just to indicate what the Positive direction of the darts is.
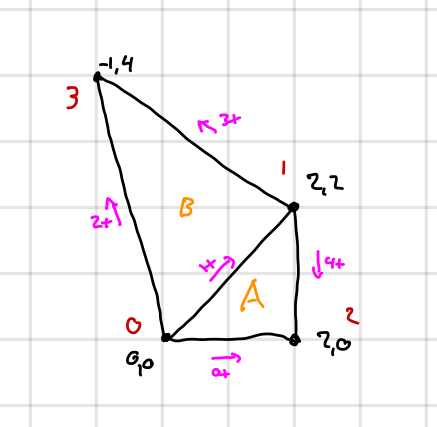
newtype PlaneGraph s v e f r Source #
Embedded, *connected*, planar graph
Constructors
| PlaneGraph (PlanarGraph s Primal (VertexData r v) e f) |
Instances
graph :: forall k (s :: k) v e f r k (s :: k) v e f r. Iso (PlaneGraph (s :: k) v e f r) (PlaneGraph (s :: k) v e f r) (PlanarGraph s 'Primal (VertexData r v) e f) (PlanarGraph s 'Primal (VertexData r v) e f) Source #
data PlanarGraph (s :: k) (w :: World) v e f #
A *connected* Planar graph with bidirected edges. I.e. the edges (darts) are directed, however, for every directed edge, the edge in the oposite direction is also in the graph.
The types v, e, and f are the are the types of the data associated with the vertices, edges, and faces, respectively.
The orbits in the embedding are assumed to be in counterclockwise order. Therefore, every dart directly bounds the face to its right.
Instances
data VertexData r v Source #
Note that the functor instance is in v
Constructors
| VertexData !(Point 2 r) !v |
Instances
vData :: forall r v v. Lens (VertexData r v) (VertexData r v) v v Source #
location :: forall r v r. Lens (VertexData r v) (VertexData r v) (Point 2 r) (Point 2 r) Source #
vtxDataToExt :: VertexData r v -> Point 2 r :+ v Source #
Arguments
| :: proxy s | |
| -> SimplePolygon p r | |
| -> f | data inside |
| -> f | data outside the polygon |
| -> PlaneGraph s p () f r |
Construct a plane graph from a simple polygon. It is assumed that the polygon is given in counterclockwise order.
the interior of the polygon will have faceId 0
pre: the input polygon is given in counterclockwise order running time: \(O(n)\).
fromConnectedSegments :: (Foldable f, Ord r, Num r) => proxy s -> f (LineSegment 2 p r :+ e) -> PlaneGraph s (NonEmpty p) e () r Source #
Constructs a connected plane graph
pre: The segments form a single connected component
running time: \(O(n\log n)\)
fromAdjacencyLists :: forall k (s :: k) (w :: World) h. (Foldable h, Functor h) => [(VertexId s w, h (VertexId s w))] -> PlanarGraph s w () () () #
Construct a planar graph from a adjacency matrix. For every vertex, all vertices should be given in counter-clockwise order.
pre: No self-loops, and no multi-edges
running time: \(O(n)\).
numVertices :: PlaneGraph s v e f r -> Int Source #
Get the number of vertices
>>>numVertices smallG4
numEdges :: PlaneGraph s v e f r -> Int Source #
Get the number of Edges
>>>numEdges smallG5
numFaces :: PlaneGraph s v e f r -> Int Source #
Get the number of faces
>>>numFaces smallG3
numDarts :: PlaneGraph s v e f r -> Int Source #
Get the number of Darts
>>>numDarts smallG10
dual :: forall k (s :: k) (w :: World) v e f. Getter (PlanarGraph s w v e f) (PlanarGraph s (DualOf w) f e v) #
Get the dual graph of this graph.
vertices' :: PlaneGraph s v e f r -> Vector (VertexId' s) Source #
Enumerate all vertices
>>>vertices' smallG[VertexId 0,VertexId 1,VertexId 2,VertexId 3]
vertices :: PlaneGraph s v e f r -> Vector (VertexId' s, VertexData r v) Source #
Enumerate all vertices, together with their vertex data
>>>mapM_ print $ vertices smallG(VertexId 0,VertexData {_location = Point2 0 0, _vData = 0}) (VertexId 1,VertexData {_location = Point2 2 2, _vData = 1}) (VertexId 2,VertexData {_location = Point2 2 0, _vData = 2}) (VertexId 3,VertexData {_location = Point2 (-1) 4, _vData = 3})
edges' :: PlaneGraph s v e f r -> Vector (Dart s) Source #
Enumerate all edges. We report only the Positive darts
edges :: PlaneGraph s v e f r -> Vector (Dart s, e) Source #
Enumerate all edges with their edge data. We report only the Positive darts.
>>>mapM_ print $ edges smallG(Dart (Arc 0) +1,"0->2") (Dart (Arc 1) +1,"0->1") (Dart (Arc 2) +1,"0->3") (Dart (Arc 4) +1,"1->2") (Dart (Arc 3) +1,"1->3")
faces :: PlaneGraph s v e f r -> Vector (FaceId' s, f) Source #
All faces with their face data.
>>>mapM_ print $ faces smallG(FaceId 0,"OuterFace") (FaceId 1,"A") (FaceId 2,"B")
internalFaces :: (Ord r, Fractional r) => PlaneGraph s v e f r -> Vector (FaceId' s, f) Source #
Reports all internal faces. running time: \(O(n)\)
faces'' :: (Ord r, Fractional r) => PlaneGraph s v e f r -> ((FaceId' s, f), Vector (FaceId' s, f)) Source #
Reports the outerface and all internal faces separately. running time: \(O(n)\)
traverseVertices :: Applicative m => (VertexId' s -> v -> m v') -> PlaneGraph s v e f r -> m (PlaneGraph s v' e f r) Source #
Traverse the vertices
(^.vertexData) $ traverseVertices (i x -> Just (i,x)) smallG Just [(VertexId 0,0),(VertexId 1,1),(VertexId 2,2),(VertexId 3,3)] >>> traverseVertices (i x -> print (i,x)) smallG >> pure () (VertexId 0,0) (VertexId 1,1) (VertexId 2,2) (VertexId 3,3)
traverseDarts :: Applicative m => (Dart s -> e -> m e') -> PlaneGraph s v e f r -> m (PlaneGraph s v e' f r) Source #
Traverses the darts
>>>traverseDarts (\d x -> print (d,x)) smallG >> pure ()(Dart (Arc 0) +1,"0->2") (Dart (Arc 0) -1,"2->0") (Dart (Arc 1) +1,"0->1") (Dart (Arc 1) -1,"1->0") (Dart (Arc 2) +1,"0->3") (Dart (Arc 2) -1,"3->0") (Dart (Arc 3) +1,"1->3") (Dart (Arc 3) -1,"3->1") (Dart (Arc 4) +1,"1->2") (Dart (Arc 4) -1,"2->1")
traverseFaces :: Applicative m => (FaceId' s -> f -> m f') -> PlaneGraph s v e f r -> m (PlaneGraph s v e f' r) Source #
Traverses the faces
>>>traverseFaces (\i x -> print (i,x)) smallG >> pure ()(FaceId 0,"OuterFace") (FaceId 1,"A") (FaceId 2,"B")
headOf :: Dart s -> PlaneGraph s v e f r -> VertexId' s Source #
The vertex this dart is heading in to
running time: \(O(1)\)
>>>headOf (dart 0 "+1") smallGVertexId 2
tailOf :: Dart s -> PlaneGraph s v e f r -> VertexId' s Source #
The tail of a dart, i.e. the vertex this dart is leaving from
running time: \(O(1)\)
>>>tailOf (dart 0 "+1") smallGVertexId 0
twin :: forall k (s :: k). Dart s -> Dart s #
Get the twin of this dart (edge)
>>>twin (dart 0 "+1")Dart (Arc 0) -1>>>twin (dart 0 "-1")Dart (Arc 0) +1
endPoints :: Dart s -> PlaneGraph s v e f r -> (VertexId' s, VertexId' s) Source #
endPoints d g = (tailOf d g, headOf d g)
running time: \(O(1)\)
>>>endPoints (dart 0 "+1") smallG(VertexId 0,VertexId 2)
incidentEdges :: VertexId' s -> PlaneGraph s v e f r -> Vector (Dart s) Source #
All edges incident to vertex v, in counterclockwise order around v.
running time: \(O(k)\), where \(k\) is the output size
>>>incidentEdges (VertexId 1) smallG[Dart (Arc 1) -1,Dart (Arc 4) +1,Dart (Arc 3) +1]
incomingEdges :: VertexId' s -> PlaneGraph s v e f r -> Vector (Dart s) Source #
All edges incident to vertex v in incoming direction (i.e. pointing into v) in counterclockwise order around v.
running time: \(O(k)\), where (k) is the total number of incident edges of v
>>>incomingEdges (VertexId 1) smallG[Dart (Arc 1) +1,Dart (Arc 4) -1,Dart (Arc 3) -1]
outgoingEdges :: VertexId' s -> PlaneGraph s v e f r -> Vector (Dart s) Source #
All edges incident to vertex v in incoming direction (i.e. pointing into v) in counterclockwise order around v.
running time: \(O(k)\), where (k) is the total number of incident edges of v
>>>outgoingEdges (VertexId 1) smallG[Dart (Arc 1) -1,Dart (Arc 4) +1,Dart (Arc 3) +1]
neighboursOf :: VertexId' s -> PlaneGraph s v e f r -> Vector (VertexId' s) Source #
Gets the neighbours of a particular vertex, in counterclockwise order around the vertex.
running time: \(O(k)\), where \(k\) is the output size
>>>neighboursOf (VertexId 1) smallG[VertexId 0,VertexId 2,VertexId 3]
nextIncidentEdge :: Dart s -> PlaneGraph s v e f r -> Dart s Source #
Given a dart d that points into some vertex v, report the next dart in the cyclic order around v in clockwise direction.
running time: \(O(1)\)
>>>nextIncidentEdge (dart 1 "+1") smallGDart (Arc 2) +1
prevIncidentEdge :: Dart s -> PlaneGraph s v e f r -> Dart s Source #
Given a dart d that points into some vertex v, report the next dart in the cyclic order around v (in clockwise order)
running time: \(O(1)\)
>>>prevIncidentEdge (dart 1 "+1") smallGDart (Arc 0) +1
leftFace :: Dart s -> PlaneGraph s v e f r -> FaceId' s Source #
The face to the left of the dart
running time: \(O(1)\).
>>>leftFace (dart 1 "+1") smallGFaceId 2>>>leftFace (dart 1 "-1") smallGFaceId 1>>>leftFace (dart 2 "+1") smallGFaceId 0>>>leftFace (dart 2 "-1") smallGFaceId 2
rightFace :: Dart s -> PlaneGraph s v e f r -> FaceId' s Source #
The face to the right of the dart
running time: \(O(1)\).
>>>rightFace (dart 1 "+1") smallGFaceId 1>>>rightFace (dart 1 "-1") smallGFaceId 2>>>rightFace (dart 2 "+1") smallGFaceId 2>>>rightFace (dart 2 "-1") smallGFaceId 0
nextEdge :: Dart s -> PlaneGraph s v e f r -> Dart s Source #
Get the next edge along the face
running time: \(O(1)\).
>>>nextEdge (dart 1 "+1") smallGDart (Arc 4) +1
prevEdge :: Dart s -> PlaneGraph s v e f r -> Dart s Source #
Get the previous edge along the face
running time: \(O(1)\).
>>>prevEdge (dart 1 "+1") smallGDart (Arc 0) -1
boundary :: FaceId' s -> PlaneGraph s v e f r -> Vector (Dart s) Source #
The darts bounding this face, for internal faces in clockwise order, for the outer face in counter clockwise order.
running time: \(O(k)\), where \(k\) is the output size.
boundary' :: Dart s -> PlaneGraph s v e f r -> Vector (Dart s) Source #
Generates the darts incident to a face, starting with the given dart.
\(O(k)\), where \(k\) is the number of darts reported
boundaryDart :: FaceId' s -> PlaneGraph s v e f r -> Dart s Source #
Gets a dart bounding this face. I.e. a dart d such that the face lies to the right of the dart.
boundaryVertices :: FaceId' s -> PlaneGraph s v e f r -> Vector (VertexId' s) Source #
The vertices bounding this face, for internal faces in clockwise order, for the outer face in counter clockwise order.
running time: \(O(k)\), where \(k\) is the output size.
outerFaceId :: (Ord r, Fractional r) => PlaneGraph s v e f r -> FaceId' s Source #
gets the id of the outer face
running time: \(O(n)\)
outerFaceDart :: (Ord r, Fractional r) => PlaneGraph s v e f r -> Dart s Source #
gets a dart incident to the outer face (in particular, that has the outerface on its left)
running time: \(O(n)\)
vertexDataOf :: VertexId' s -> Lens' (PlaneGraph s v e f r) (VertexData r v) Source #
locationOf :: VertexId' s -> Lens' (PlaneGraph s v e f r) (Point 2 r) Source #
General interface to accessing vertex data, dart data, and face data.
Methods
dataOf :: i -> Lens' g (DataOf g i) #
get the data associated with the value i.
running time: \(O(1)\) to read the data, \(O(n)\) to write it.
Instances
endPointsOf :: Dart s -> Getter (PlaneGraph s v e f r) (VertexData r v, VertexData r v) Source #
Getter for the data at the endpoints of a dart
running time: \(O(1)\)
endPointData :: Dart s -> PlaneGraph s v e f r -> (VertexData r v, VertexData r v) Source #
Data corresponding to the endpoints of the dart
running time: \(O(1)\)
vertexData :: Lens (PlaneGraph s v e f r) (PlaneGraph s v' e f r) (Vector v) (Vector v') Source #
faceData :: Lens (PlaneGraph s v e f r) (PlaneGraph s v e f' r) (Vector f) (Vector f') Source #
Lens to access face data
dartData :: Lens (PlaneGraph s v e f r) (PlaneGraph s v e' f r) (Vector (Dart s, e)) (Vector (Dart s, e')) Source #
lens to access the Dart Data
rawDartData :: Lens (PlaneGraph s v e f r) (PlaneGraph s v e' f r) (Vector e) (Vector e') Source #
Lens to access the raw dart data, use at your own risk
edgeSegment :: Dart s -> PlaneGraph s v e f r -> LineSegment 2 v r :+ e Source #
Given a dart and the graph constructs the line segment representing the dart. The segment \(\overline{uv})\) is has \(u\) as its tail and \(v\) as its head.
\(O(1)\)
edgeSegments :: PlaneGraph s v e f r -> Vector (Dart s, LineSegment 2 v r :+ e) Source #
Reports all edges as line segments
>>>mapM_ print $ edgeSegments smallG(Dart (Arc 0) +1,ClosedLineSegment (Point2 0 0 :+ 0) (Point2 2 0 :+ 2) :+ "0->2") (Dart (Arc 1) +1,ClosedLineSegment (Point2 0 0 :+ 0) (Point2 2 2 :+ 1) :+ "0->1") (Dart (Arc 2) +1,ClosedLineSegment (Point2 0 0 :+ 0) (Point2 (-1) 4 :+ 3) :+ "0->3") (Dart (Arc 4) +1,ClosedLineSegment (Point2 2 2 :+ 1) (Point2 2 0 :+ 2) :+ "1->2") (Dart (Arc 3) +1,ClosedLineSegment (Point2 2 2 :+ 1) (Point2 (-1) 4 :+ 3) :+ "1->3")
rawFacePolygon :: FaceId' s -> PlaneGraph s v e f r -> SimplePolygon v r :+ f Source #
Alias for rawFace Boundary
runningtime: \(O(k)\), where \(k\) is the size of the face.
rawFaceBoundary :: FaceId' s -> PlaneGraph s v e f r -> SimplePolygon v r :+ f Source #
The polygon describing the face
runningtime: \(O(k)\), where \(k\) is the size of the face.
rawFacePolygons :: PlaneGraph s v e f r -> Vector (FaceId' s, SimplePolygon v r :+ f) Source #
Lists all faces of the plane graph.
newtype VertexId (s :: k) (w :: World) #
A vertex in a planar graph. A vertex is tied to a particular planar graph by the phantom type s, and to a particular world w.
Constructors
| VertexId | |
Fields
| |
Instances
newtype FaceId (s :: k) (w :: World) #
The type to represent FaceId's
Instances
A dart represents a bi-directed edge. I.e. a dart has a direction, however the dart of the oposite direction is always present in the planar graph as well.
Instances
The world in which the graph lives
withEdgeDistances :: (Point 2 r -> Point 2 r -> a) -> PlaneGraph s p e f r -> PlaneGraph s p (a :+ e) f r Source #
Labels the edges of a plane graph with their distances, as specified by the distance function.