{#measures}
============
Measuring Data Types
--------------------
\begin{code}
module Measures where
import Prelude hiding ((!!), length)
import Language.Haskell.Liquid.Prelude
length :: L a -> Int
(!) :: L a -> Int -> a
insert :: Ord a => a -> L a -> L a
insertSort :: Ord a => [a] -> L a
infixr `C`
\end{code}
Measuring Data Types
====================
Recap
-----
1. **Refinements:** Types + Predicates
2. **Subtyping:** SMT Implication
Example: Length of a List
-------------------------
Given a type for lists:
\begin{code}
data L a = N | C a (L a)
\end{code}
We can define the **length** as:
\begin{code}
{-@ measure llen :: (L a) -> Int
llen (N) = 0
llen (C x xs) = 1 + (llen xs) @-}
\end{code}
Example: Length of a List
-------------------------
\begin{code}
{-@ measure llen :: (L a) -> Int
llen (N) = 0
llen (C x xs) = 1 + (llen xs) @-}
\end{code}
We **strengthen** data constructor types
\begin{code}
data L a where
N :: {v: L a | (llen v) = 0}
C :: a -> t:_ -> {v:_| llen v = 1 + llen t}
\end{code}
Measures Are Uninterpreted
--------------------------
\begin{code}
data L a where
N :: {v: L a | (llen v) = 0}
C :: a -> t:_ -> {v:_| llen v = 1 + llen t}
\end{code}
`llen` is an **uninterpreted function** in SMT logic
Measures Are Uninterpreted
--------------------------
In SMT, [uninterpreted function](http://fm.csl.sri.com/SSFT12/smt-euf-arithmetic.pdf) $f$ obeys **congruence** axiom:
$$\forall \overline{x}, \overline{y}. \overline{x} = \overline{y} \Rightarrow
f(\overline{x}) = f(\overline{y})$$
Other properties of `llen` asserted when typing **fold** & **unfold**
Crucial for *efficient*, *decidable* and *predictable* verification.
Measures Are Uninterpreted
--------------------------
Other properties of `llen` asserted when typing **fold** & **unfold**
\begin{code}**Fold**
z = C x y -- z :: {v | llen v = 1 + llen y}
\end{code}
\begin{code}**Unfold**
case z of
N -> e1 -- z :: {v | llen v = 0}
C x y -> e2 -- z :: {v | llen v = 1 + llen y}
\end{code}
Measured Refinements
--------------------
Now, we can verify:
\begin{code}
{-@ length :: xs:L a -> (EqLen xs) @-}
length N = 0
length (C _ xs) = 1 + length xs
\end{code}
Where `EqLen` is a type alias:
\begin{code}
{-@ type EqLen Xs = {v:Nat | v = (llen Xs)} @-}
\end{code}
List Indexing Redux
-------------------
We can type list lookup:
\begin{code}
{-@ (!) :: xs:L a -> (LtLen xs) -> a @-}
(C x _) ! 0 = x
(C _ xs) ! i = xs ! (i - 1)
_ ! _ = liquidError "never happens!"
\end{code}
Where `LtLen` is a type alias:
\begin{code}
{-@ type LtLen Xs = {v:Nat | v < (llen Xs)} @-}
\end{code}
Demo:
What if we *remove* the precondition?
Support **many** measures on a type ...
... by **conjoining** the constructor refinements.
[[Skip...]](#/refined-data-cons)
Multiple Measures: Red-Black Trees
==================================
{#rbtree}
----------
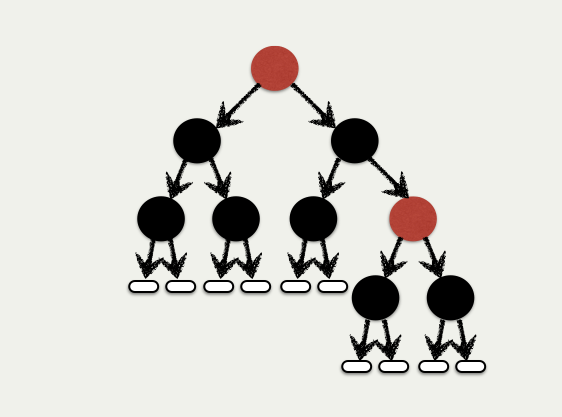 +
+ **Color:** `Red` nodes have `Black` children
+ **Height:** Number of `Black` nodes equal on *all paths*
[[Skip...]](#/refined-data-cons)
Basic Type
----------
\begin{code}
data Tree a = Leaf
| Node Color a (Tree a) (Tree a)
data Color = Red
| Black
\end{code}
Color Invariant
---------------
`Red` nodes have `Black` children
\begin{code}
measure isRB :: Tree a -> Prop
isRB (Leaf) = true
isRB (Node c x l r) = c=Red => (isB l && isB r)
&& isRB l && isRB r
\end{code}
\begin{code} where
measure isB :: Tree a -> Prop
isB (Leaf) = true
isB (Node c x l r) = c == Black
\end{code}
*Almost* Color Invariant
------------------------
Color Invariant **except** at root.
\begin{code}
measure isAlmost :: Tree a -> Prop
isAlmost (Leaf) = true
isAlmost (Node c x l r) = isRB l && isRB r
\end{code}
Height Invariant
----------------
Number of `Black` nodes equal on **all paths**
\begin{code}
measure isBH :: RBTree a -> Prop
isBH (Leaf) = true
isBH (Node c x l r) = bh l = bh r
&& isBH l && isBH r
\end{code}
\begin{code} where
measure bh :: RBTree a -> Int
bh (Leaf) = 0
bh (Node c x l r) = bh l
+ if c = Red then 0 else 1
\end{code}
Refined Type
------------
\begin{code}
-- Red-Black Trees
type RBT a = {v:Tree a | isRB v && isBH v}
-- Almost Red-Black Trees
type ARBT a = {v:Tree a | isAlmost v && isBH v}
\end{code}
[Details](https://github.com/ucsd-progsys/liquidhaskell/blob/master/tests/pos/RBTree.hs)
Refined Data Constructors
=========================
{#refined-data-cons}
---------------------
Can encode invariants **inside constructors**
\begin{code}
{-@ data L a = N
| C { x :: a
, xs :: L {v:a| x <= v} } @-}
\end{code}
Head `x` is less than **every** element of tail `xs`
i.e. specifies **increasing** Lists
Increasing Lists
----------------
\begin{code}
data L a where
N :: L a
C :: x:a -> xs: L {v:a | x <= v} -> L a
\end{code}
- We **check** property when **folding** `C`
- We **assume** property when **unfolding** `C`
Increasing Lists
----------------
Demo: Insertion Sort (hover for inferred types)
\begin{code}
insertSort = foldr insert N
insert y (x `C` xs)
| y <= x = y `C` (x `C` xs)
| otherwise = x `C` insert y xs
insert y N = y `C` N
\end{code}
**Problem 1:** What if we need [increasing & decreasing lists](http://web.cecs.pdx.edu/~sheard/Code/QSort.html)?
Recap
-----
1. Refinements: Types + Predicates
2. Subtyping: SMT Implication
3. **Measures:** Strengthened Constructors
- **Decouple** property from structure
 +
+