Red-Black Trees
===============
\begin{code}
{-@ LIQUID "--no-termination" @-}
{-@ LIQUID "--diff" @-}
module RBTree (ok, bad1, bad2) where
import Language.Haskell.Liquid.Prelude
ok, bad1, bad2 :: RBTree Int
---------------------------------------------------------------------------
-- | Specifications -------------------------------------------------------
---------------------------------------------------------------------------
-- | Red-Black Trees
{-@ type RBT a = {v: RBTree a | isRB v && isBH v } @-}
{-@ measure isRB :: RBTree a -> Prop
isRB (Leaf) = true
isRB (Node c x l r) = isRB l && isRB r && (c == R => (IsB l && IsB r))
@-}
-- | Almost Red-Black Trees
{-@ type ARBT a = {v: RBTree a | isARB v && isBH v} @-}
{-@ measure isARB :: (RBTree a) -> Prop
isARB (Leaf) = true
isARB (Node c x l r) = (isRB l && isRB r)
@-}
-- | Color of a tree
{-@ measure col :: RBTree a -> Color
col (Node c x l r) = c
col (Leaf) = B
@-}
{-@ measure isB :: RBTree a -> Prop
isB (Leaf) = false
isB (Node c x l r) = c == B
@-}
{-@ predicate IsB T = not (col T == R) @-}
-- | Black Height
{-@ measure isBH :: RBTree a -> Prop
isBH (Leaf) = true
isBH (Node c x l r) = (isBH l && isBH r && bh l = bh r)
@-}
{-@ measure bh :: RBTree a -> Int
bh (Leaf) = 0
bh (Node c x l r) = bh l + if (c == R) then 0 else 1
@-}
-- | Binary Search Ordering
{-@ data RBTree a = Leaf
| Node { c :: Color
, key :: a
, left :: RBTree ({v:a | v < key})
, right :: RBTree ({v:a | key < v}) } @-}
\end{code}
{#asdad}
---------
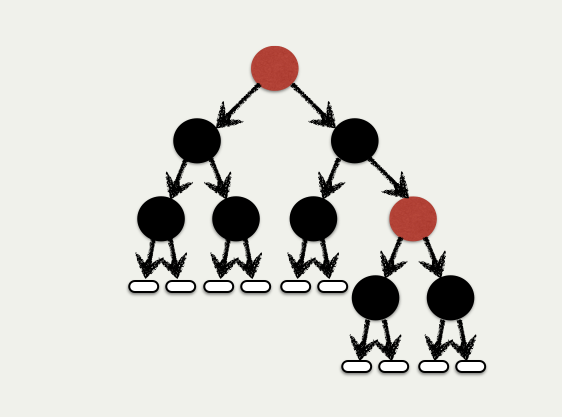 +
+ **Color Invariant:** `Red` nodes have `Black` children
+ **Height Invariant:** Number of `Black` nodes equal on *all paths*
+ **Order Invariant:** Left keys < root < Right keys
Basic Type
----------
\begin{code}
data Color = R | B
data RBTree a = Leaf
| Node { c :: Color
, key :: a
, left :: RBTree a
, right :: RBTree a }
\end{code}
1. Color Invariant
------------------
`Red` nodes have `Black` children
\begin{spec}
measure isRB :: Tree a -> Prop
isRB (Leaf) = true
isRB (Node c x l r) = c == R => (isB l && isB r)
&& isRB l && isRB r
\end{spec}
where
\begin{spec}
measure isB :: Tree a -> Prop
isB (Leaf) = true
isB (Node c x l r) = c == B
\end{spec}
1. *Almost* Color Invariant
---------------------------
Color Invariant **except** at root.
\begin{spec}
measure isAlmost :: RBTree a -> Prop
isAlmost (Leaf) = true
isAlmost (Node c x l r) = isRB l && isRB r
\end{spec}
2. Height Invariant
-------------------
Number of `Black` nodes equal on **all paths**
\begin{spec}
measure isBH :: RBTree a -> Prop
isBH (Leaf) = true
isBH (Node c x l r) = bh l == bh r
&& isBH l && isBH r
\end{spec}
where
\begin{spec}
measure bh :: RBTree a -> Int
bh (Leaf) = 0
bh (Node c x l r) = bh l
+ if c == R then 0 else 1
\end{spec}
3. Order Invariant
------------------
**Binary Search Ordering**
\begin{spec}
data RBTree a
= Leaf
| Node { c :: Color
, key :: a
, left :: RBTree {v:a | v < key}
, right :: RBTree {v:a | key < v}
}
\end{spec}
Valid Red-Black Trees
---------------------
**Conjoining Specifications**
\begin{spec}
-- | Red-Black Trees
type RBT a = {v:RBTree a|isRB v && isBH v}
-- | Almost Red-Black Trees
type ARBT a = {v:RBTree a|isAlmost v && isBH v}
\end{spec}
[Details](https://github.com/ucsd-progsys/liquidhaskell/blob/master/tests/pos/RBTree.hs)
Ex: Satisfies Invariants
-------------------------
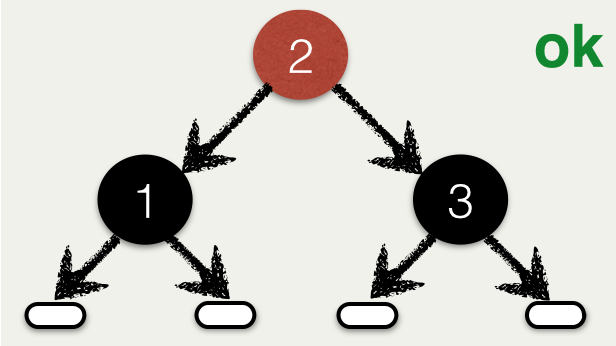
\begin{code}
{-@ ok :: RBT Int @-}
ok = Node R 2
(Node B 1 Leaf Leaf)
(Node B 3 Leaf Leaf)
\end{code}
Ex: Violates Order Invariant
----------------------------
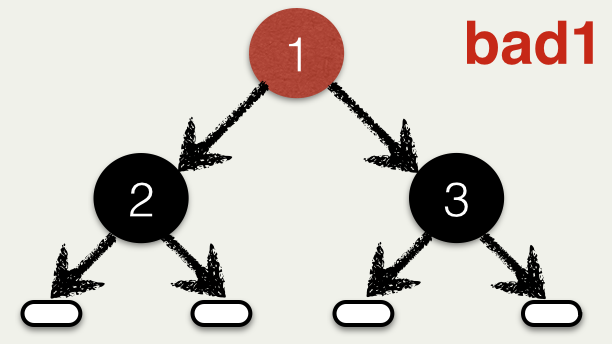
\begin{code}
{-@ bad1 :: RBT Int @-}
bad1 = Node R 1
(Node B 2 Leaf Leaf)
(Node B 3 Leaf Leaf)
\end{code}
Ex: Violates Color Invariant
----------------------------
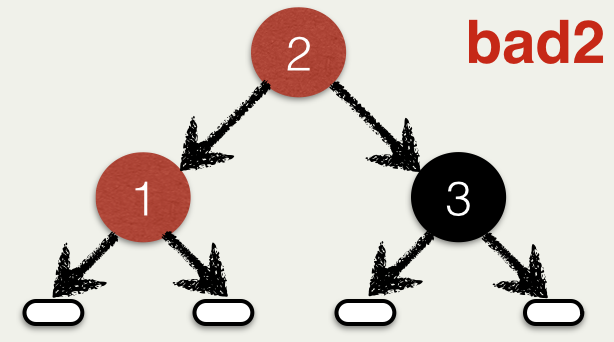
\begin{code}
{-@ bad2 :: RBT Int @-}
bad2 = Node R 2
(Node R 1 Leaf Leaf)
(Node B 3 Leaf Leaf)
\end{code}
Verified Red-Black Operations
-----------------------------
**Types Verify Correctness of**
+ Insertion
+ Deletion
+ Lookup ...
**In presence of rotation & rebalancing** [[details]](https://github.com/ucsd-progsys/liquidhaskell/blob/master/tests/pos/RBTree.hs)
 +
+ 

